미분가능한 환경을 찾아서
Abstract
- 건축 알고리즘, 혹은 패러메트릭 디자인을 수행한다는 것은 파라미터에 따른 결과를 만들어내는 알고리즘이라 생각을 고정하기 쉽습니다.
- 하지만 ga 나 es 같은 heuristic optimizer 에서는 그 알고리즘 자체가 파라미터를 변경하고자 하는 환경으로,
- 더욱이 모델이 학습의 기준으로 사용하기 위한 환경으로 사용되며, 강화 학습이 될 경우, 환경은 모델의 방향성을 판단하는 기준 그 자체가 됩니다.
- 이 때, 환경은 어떤 특성을 지녀야 하는가에 대한 탐구의 일환으로, 미분가능한 환경의 의의를 찾고 결과를 테스트해봤습니다.
- gradient 단절이 확실한 환경과 그렇지 않은 환경 두 환경을 설정하고
- 실제로 미분 가능한 환경일 때 사용이 가능한 gradient descent 및 AdamW 방법을 포함해, ga 를 비교해 미분 가능한 환경의 의의를 확인할 수 있었습니다.
Problem
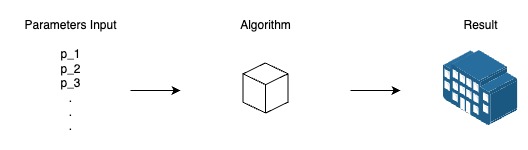
건축 알고리즘 관련 환경을 작성한다 - 혹은 패러메트릭 디자인 환경을 작성한다 - 는 것은 직관적으로는 다음과 같은 형식을 가지고 있습니다.
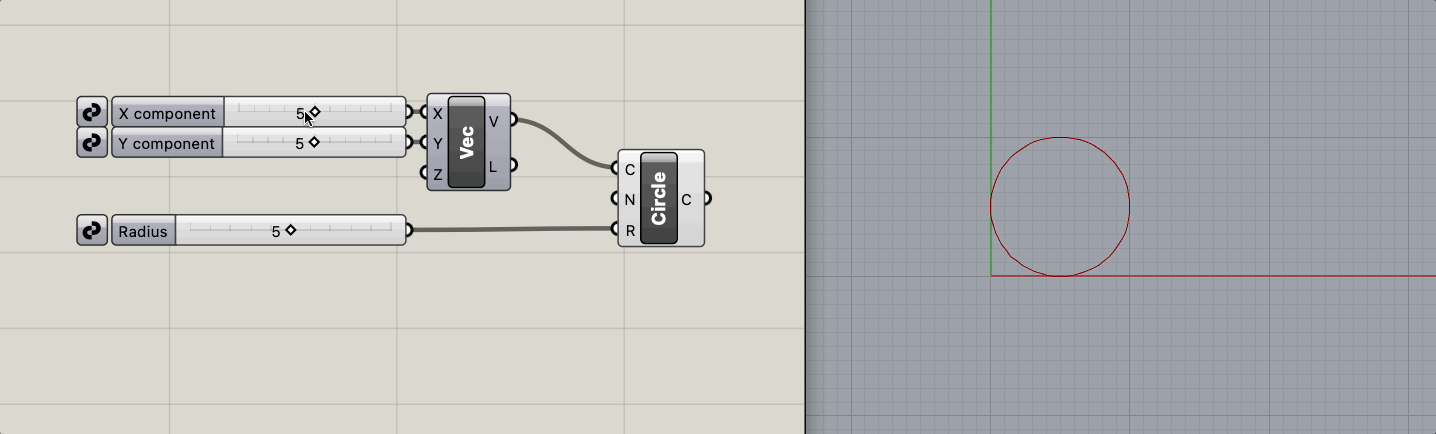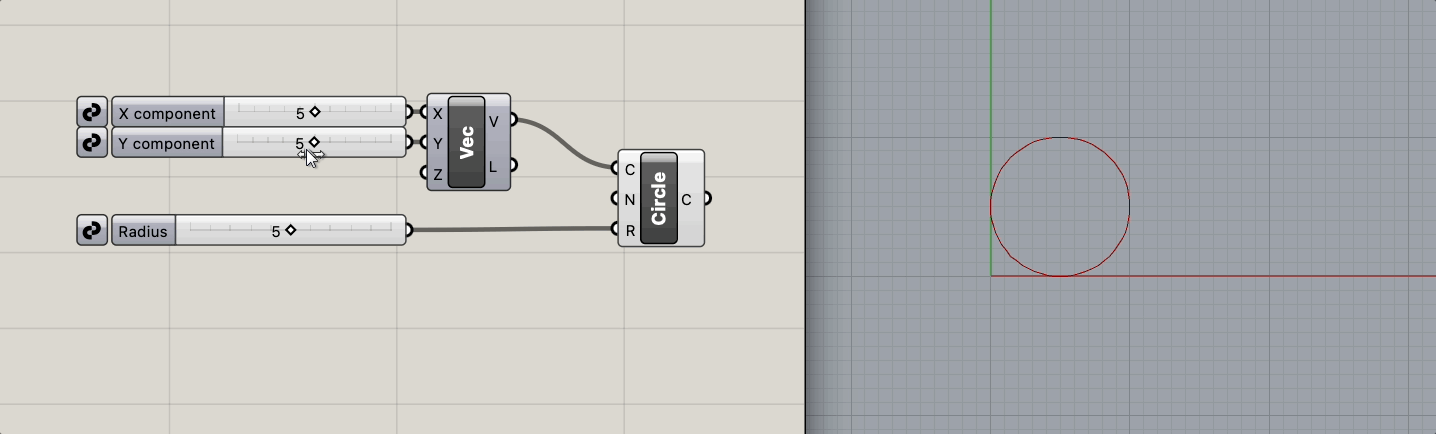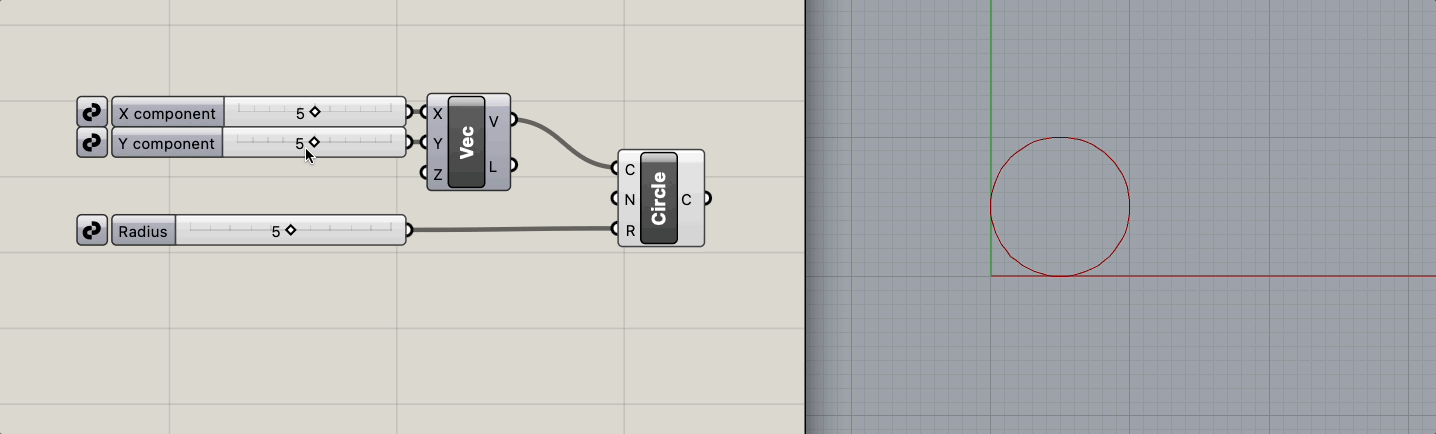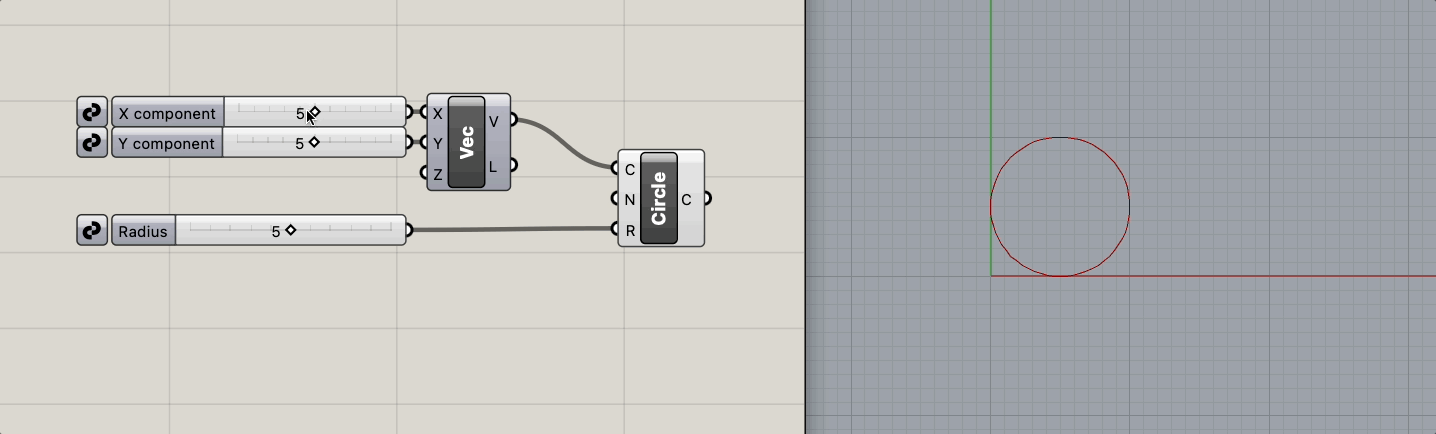
원의 위치와 반지름을 파라미터로 원을 생성한다.
loss 는 원의 넓이와 반지름 5인 경우의 원의 넓이(25)와의 차이의 10분의 1로 정의한다.
위처럼 로직이 단순할 떄는 파라미터와 결과 사이의 직관성이 크게 떨어지는 일은 많지 않을 것입니다.
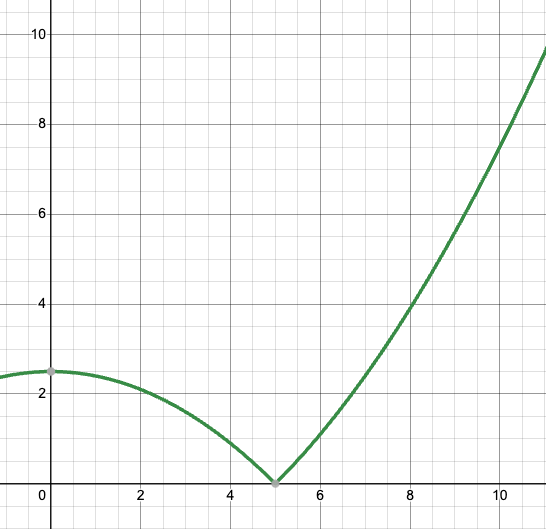
그 때의 radius - loss 그래프와 같이 표현하면 다음과 같습니다. (x >= 0 인 경우)
하지만 알고리즘이 점점 복잡해질수록 이 환경은 블랙박스가 되어가고,
사용자는 물론 이를 개발한 사람 조차도 파라미터에 따른 결과의 경향성 조차 파악하기 어려워집니다.
이 때 문제가 발생합니다.
- 강화학습의 모델까지 생각할 것도 없이, ga와 같은 최적화 과정에서도 파라미터 변경에 따른 결과의 “측정”은 필요합니다.
- 하지만 파라미터의 차이가 환경에 미칠 영향의 랜덤성이 너무 커 파라미터 변경에 따른 결과 역시 지나치게 랜덤해집니다.
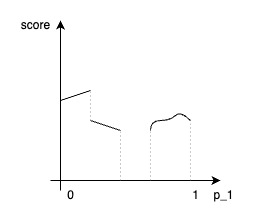
위의 그림은 파라미터 하나의 경우에만의 예시인데도 문제가 바로 보입니다. 하지만 건축 알고리즘 관련 엔진에서는 당연히 파라미터를 한두개 사용하는 것으로 끝낼 수 있는 경우는 존재하지 않습니다. 그러면 다음과 같은 경향을 확인할 수 있는 부드러운 곡면은 물론이고, 최적화 모듈은 경향성을 파악하는 것이 사실상 불가능에 가깝다는 것입니다.
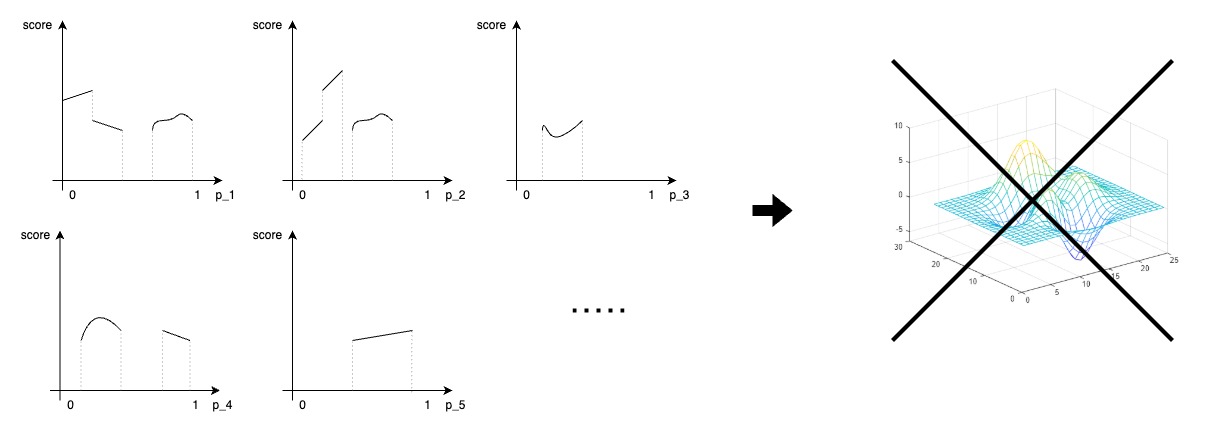continuous 한 [parameter - loss] 없이 continuous 한 엔진은 없습니다.
따라서, 어떠한 환경의 기능 및 파라미터를 추가할 때, 그 파라미터와 파라미터에 대응하는 환경이 만드는 score (혹은 loss 의 음수) 가 미분 가능한 관계가 될 수 있도록 의식적으로 추가해보는 것으로 시작해보았습니다.
Premises
- 패러메트릭 디자인 알고리즘을 포함해, 이 포스트에서 말하는 환경은 파라미터를 입력해 결과 geometry 관련 데이터 및 loss까지 계산할 수 있는 모듈을 의미한다.
- 미분 가능함 혹은 파라미터의 연결성을 명시적으로 보장하기 위해, starting parameter 에서 loss 계산까지의 모든 과정은 torch 의 tensor 연산으로만 이루어진다.
Environment Details
1. 사용할 파라미터와 및 loss 등 환경 정의
- 파라미터 정의 - 총 16개
- 환경 1 - 4개의 사각형의 x, y position ratio
- (x_ratio, y_ratio) 는 각 사각형의 width 와 height 를 기준으로 하며, (x, y) 위치와 일대일 대응하는 것을 위함입니다.
- (x_ratio, y_ratio) 는 각 사각형의 width 와 height 를 기준으로 하며, (x, y) 위치와 일대일 대응하는 것을 위함입니다.
- 환경 2 - 4개의 사각형의 interpolation, offset ratio
- offset은 해당하는 width 혹은 height 의 0.5를 기준으로 작동해, (interpolation, offset ratio)는 이를 통해 생성한 (x, y) 위치와 일대일 대응하는 것을 위함입니다.
- 즉, gradient 단절이 확실히 존재합니다.
- 환경 1 - 4개의 사각형의 x, y position ratio
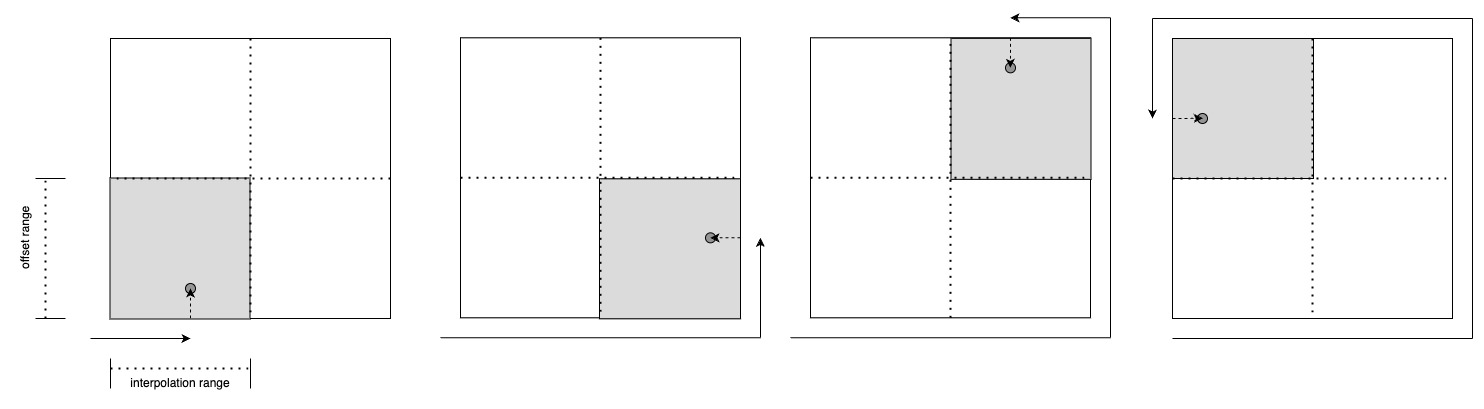Environment 2 의 4개 사분면 분리를 위한 0.5 사용
- 공통 - 4개의 사각형의 x, y size ratio - position 이 정해진 후 남은 가능 거리 중에서 비율을 통해 x_size 와 y_size 를 결정합니다.
- 즉, 두 환경 모두 동일한 2D 평면의 모든 점 (x, y) ∈ ℝ² 에 대해, 이를 생성할 수 있는 파라미터가 일대일 대응으로 존재해, 두 환경은 동일한 탐색 영역을 바라보고 있습니다.
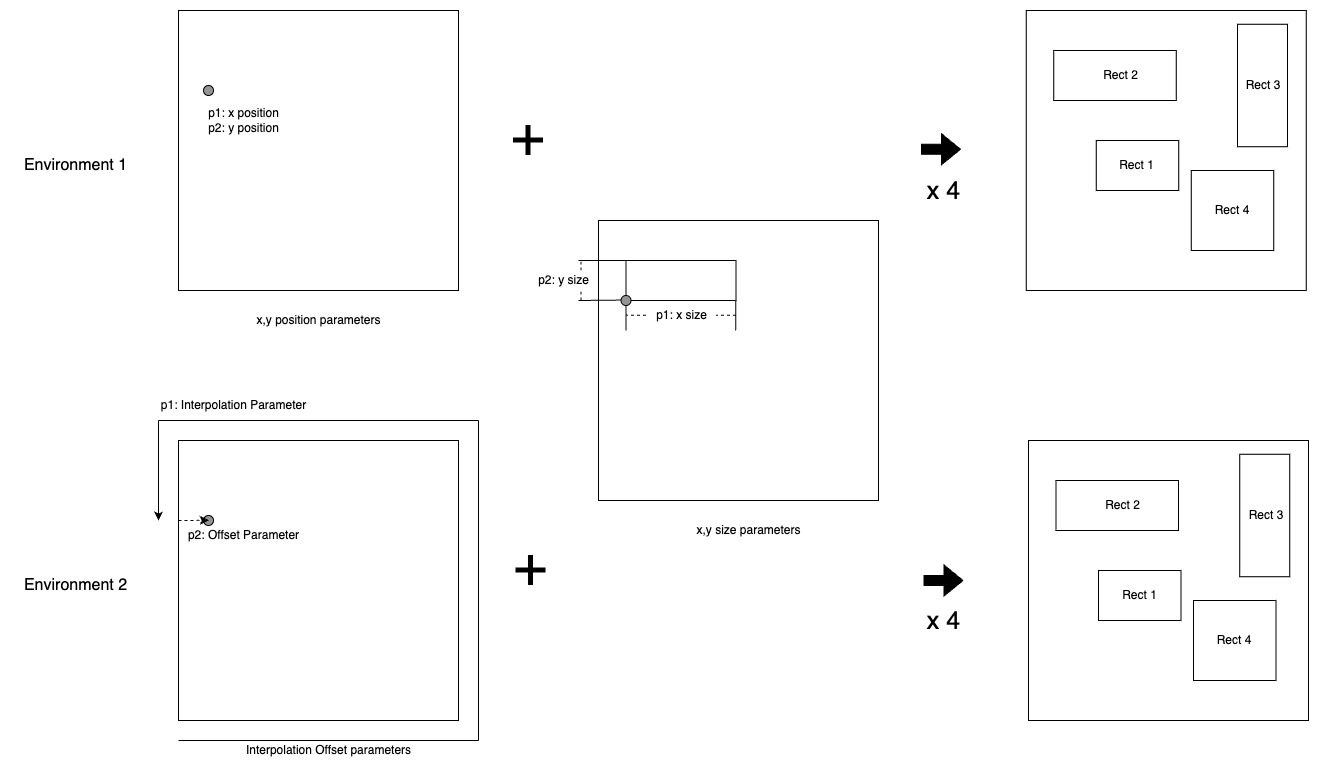
- loss 정의 (각 loss 는 추가로 계수가 곱해져 최종 loss에 더해진다.)
- L1: 각 사각형의 넓이의 분산 (각 사각형이 서로 비슷한 면적을 가지도록)
$$ \displaystyle L1 = \frac{1}{n} \sum_{i=1}^{n} (Area(Rectangle_i) - \mu)^2 $$- L2: 각 사각형의 서로 겹치는 넓이의 합 (각 사각형이 서로 겹치지 않도록)
$$ \displaystyle L2 = \sum_{i=1}^{n} \sum_{j=i+1}^{n} Area(Rectangle_i \cap Rectangle_j) $$- L3: 각 사각형의 aspect ratio (1.5에서 벗어나는 정도)
$$ \displaystyle L3 = \sum_{i=1}^{n} \left| \frac{\max(w_i, h_i)}{\min(w_i, h_i)} - 1.5 \right| $$- L4: 각 사각형의 면적의 합 (면적이 커져야 한다.)
$$ \displaystyle L4 = \sum_{i=1}^{n} Area(Rectangle_i) $$
원시적인 Gradient Descent 사용을 통한 미분 가능 정도 확인
# 학습 모델의 가중치를 변경하는 optimizer 가 아니라,
# 결과 생성에 사용하고자 하는 parameter 를 직접 update하는 differentialbe programming 입니다.
optimizer = torch.optim.SGD([parameters], lr=learning_rate)
- parameter 는 0 ~ 1 범위를 사용하도록 sigmoid 가 사용되었습니다.
- back propagation 된 grad 를 parameter 에 단순 반영하는 방법으로, 양쪽의 환경에서 간단하게 테스트해보았습니다.
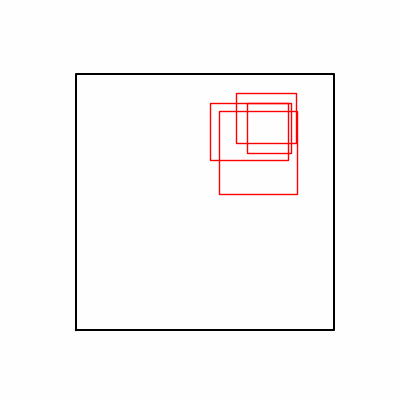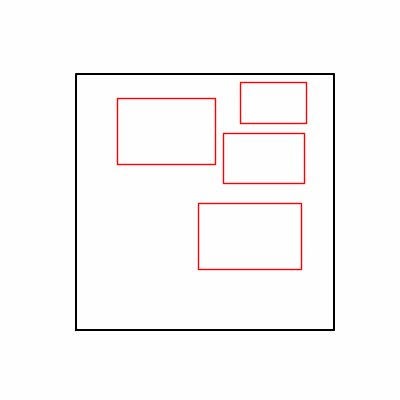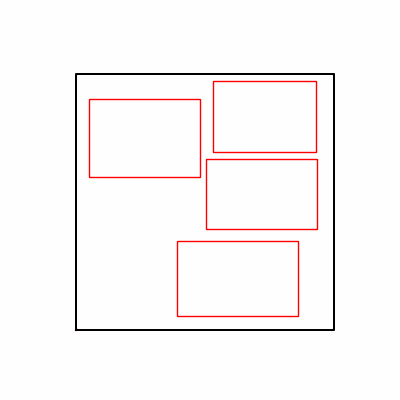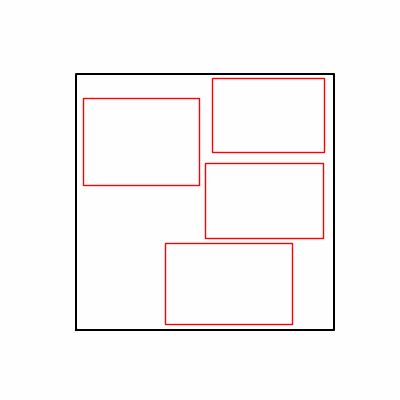
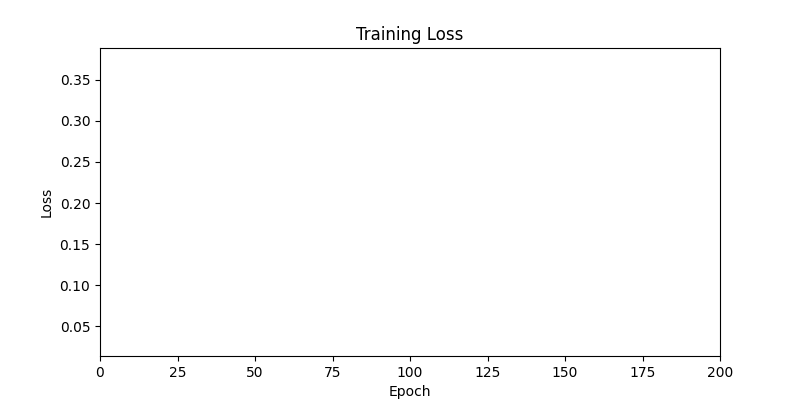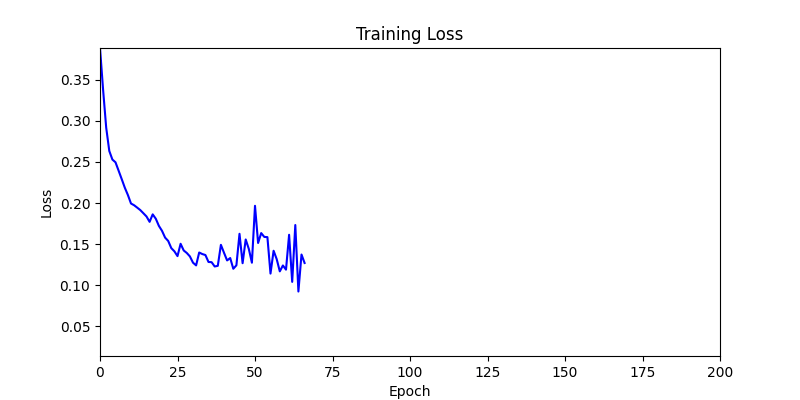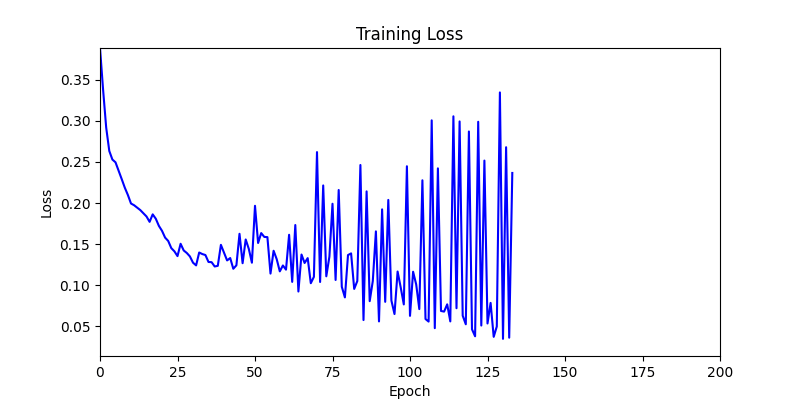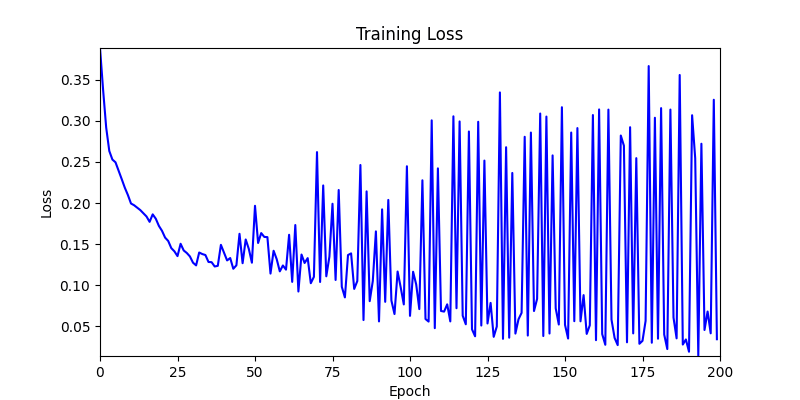
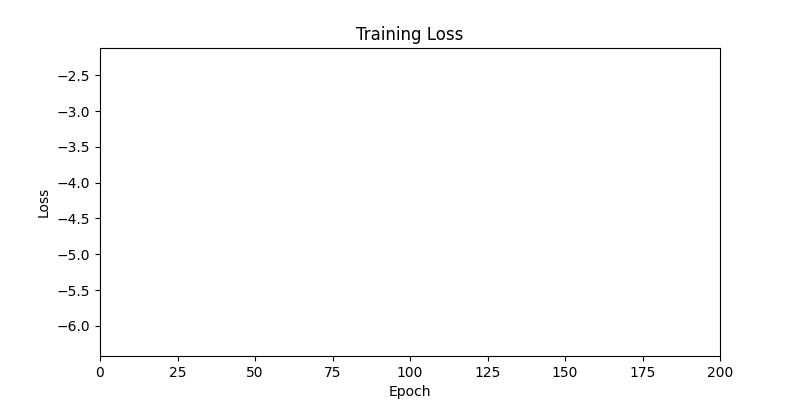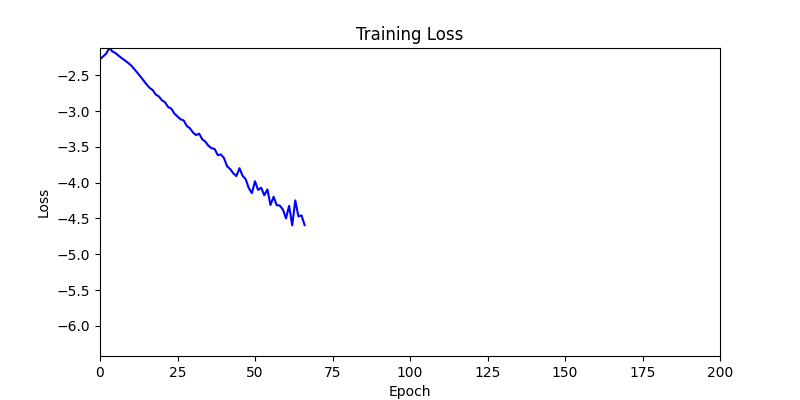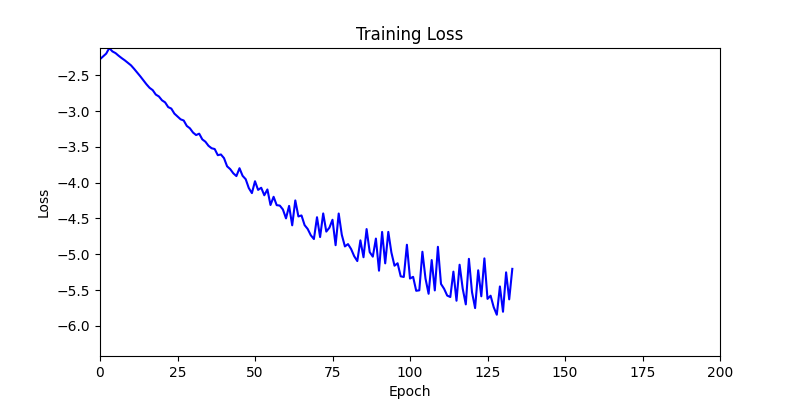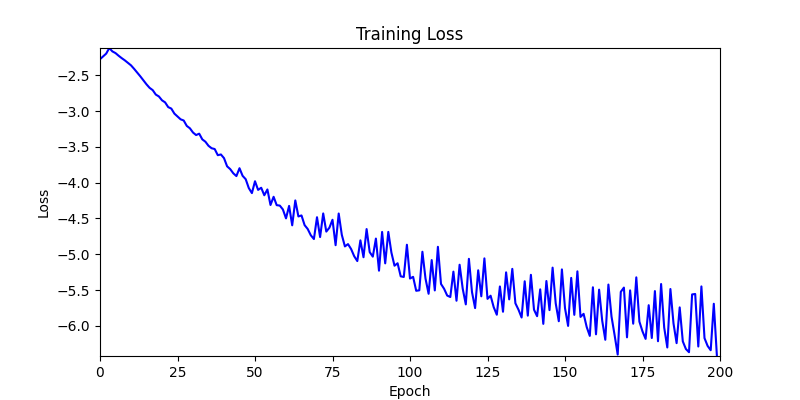
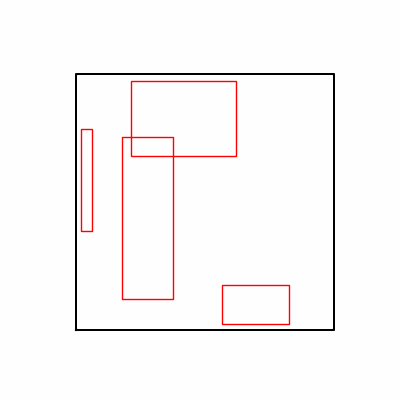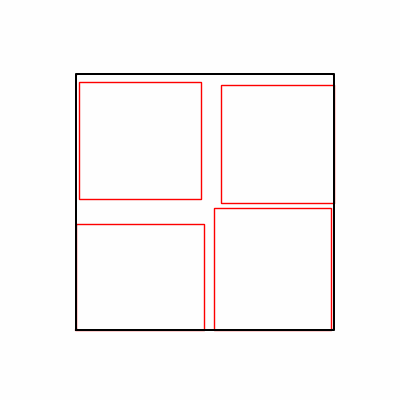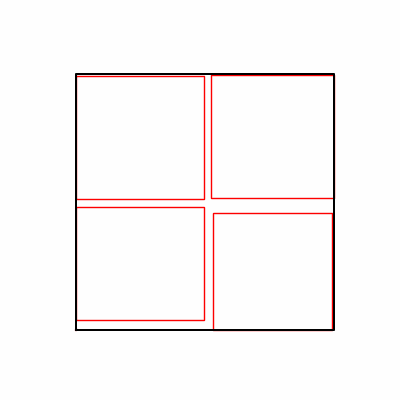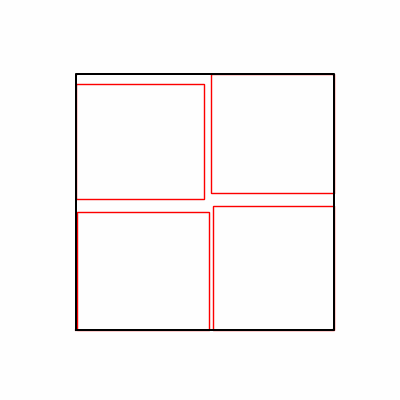
- 환경 1이 더 상대적으로 더 일관적인 경향성을 보이고, 최종 loss 값도 더 작으며, 실제 도형 배치 역시 의도에 가까운 결과를 보여주었습니다.
- (다만, Loss 는 현재 완전하다기보다 테스트의 경향을 파악하기 위함으로, 실제 도형 배치 이미지 자체보다 Loss 숫자 자체에 더 중점을 두겠습니다.)
- (다만, Loss 는 현재 완전하다기보다 테스트의 경향을 파악하기 위함으로, 실제 도형 배치 이미지 자체보다 Loss 숫자 자체에 더 중점을 두겠습니다.)
- 즉, 두 환경 모두 바라보고 있는 탐색 영역은 동일하지만 환경 1이 더 미분가능한 환경에 가깝다고 볼 수 있습니다.
- 환경 1
Loss 1
Loss 2
Loss 3
Loss 4
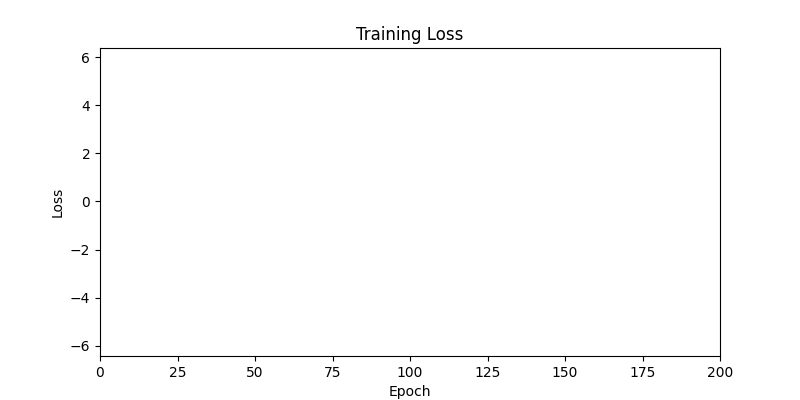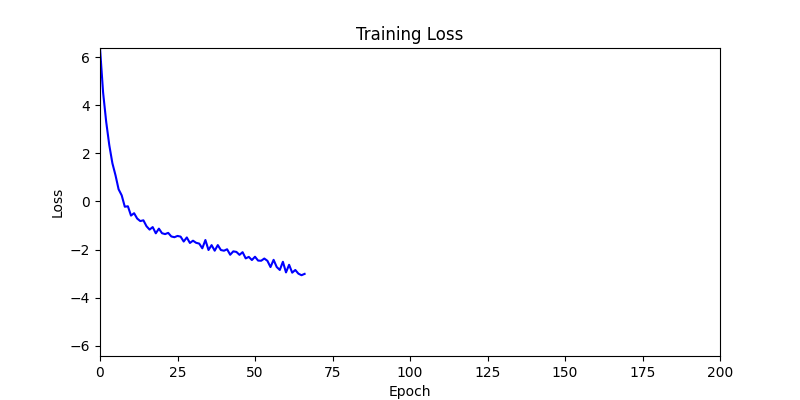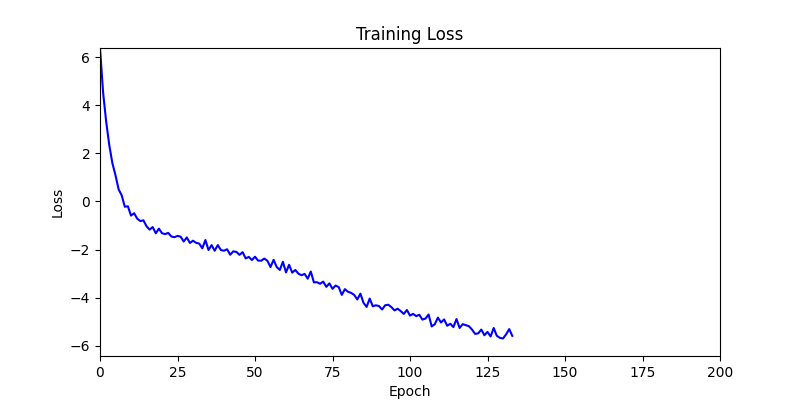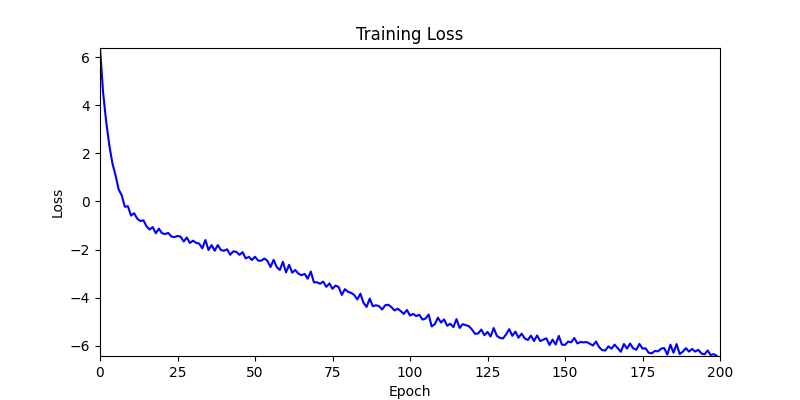
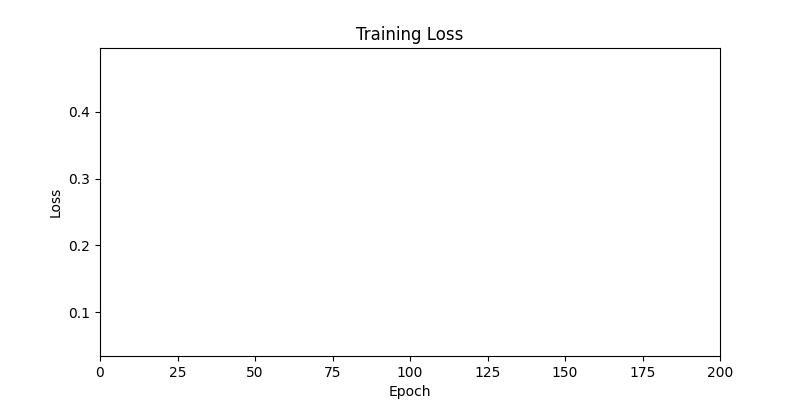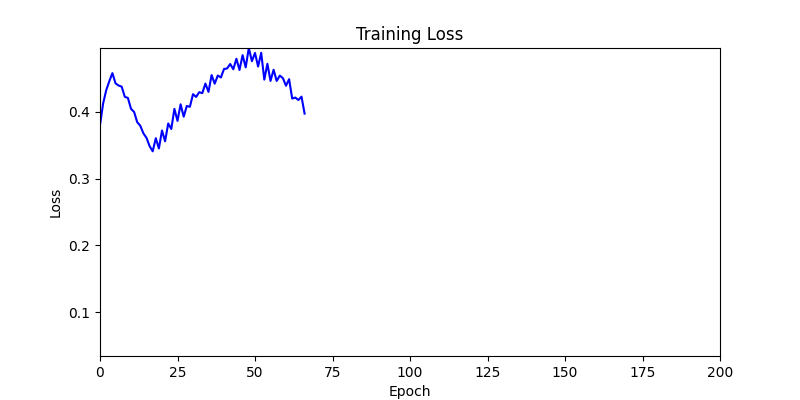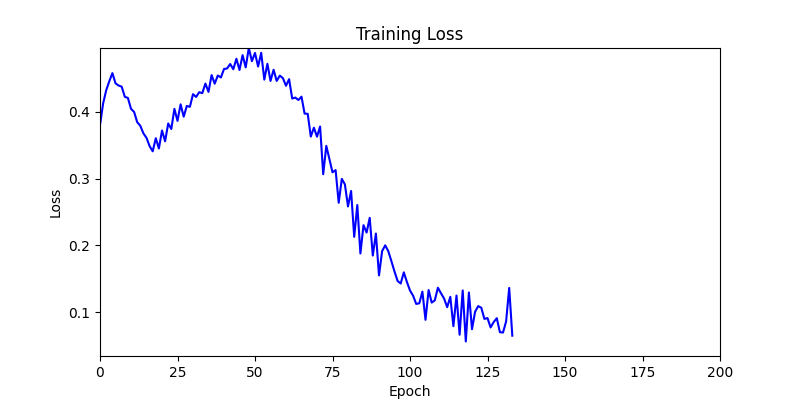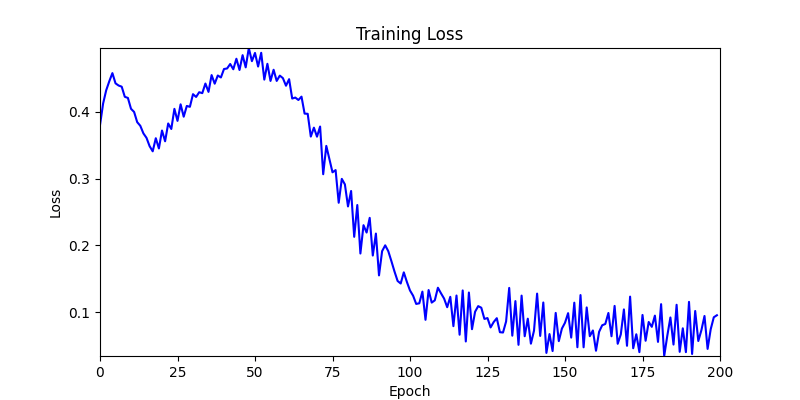
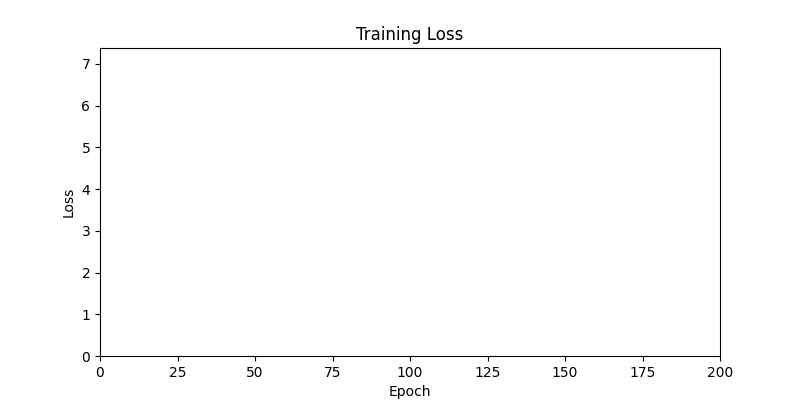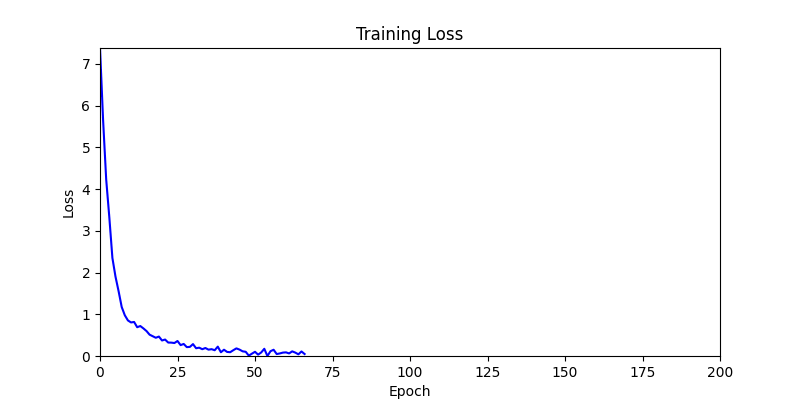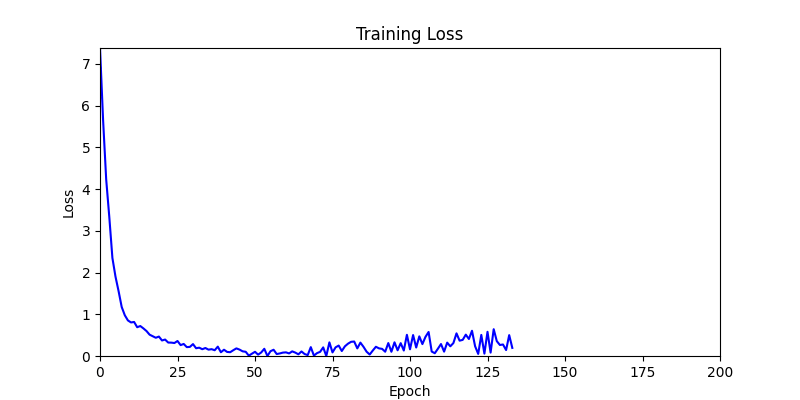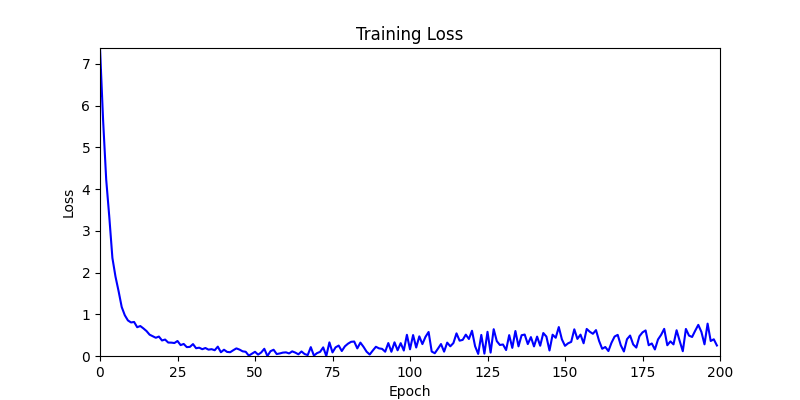
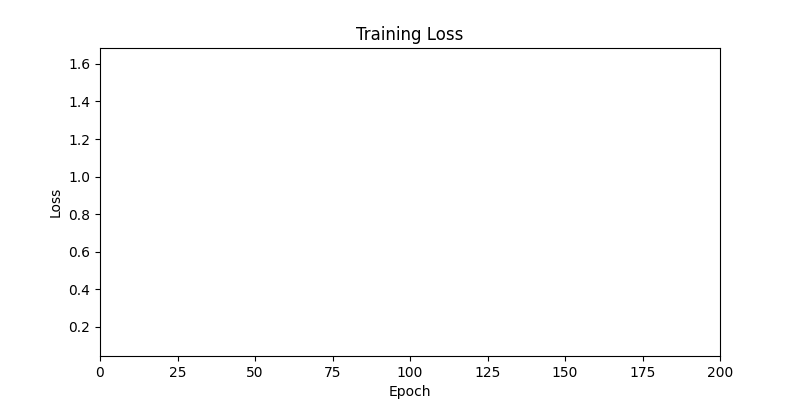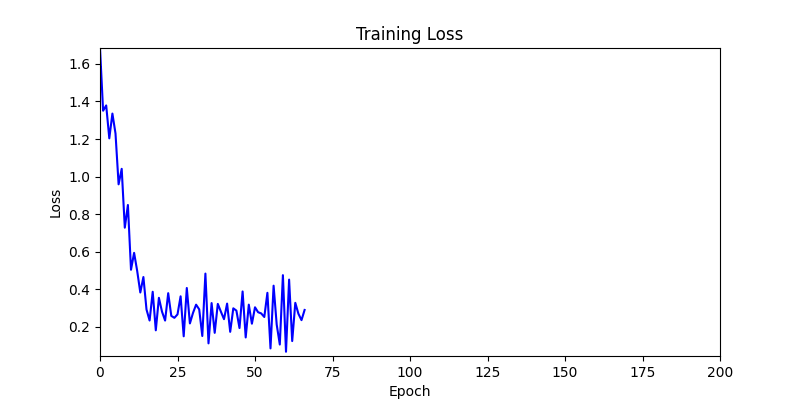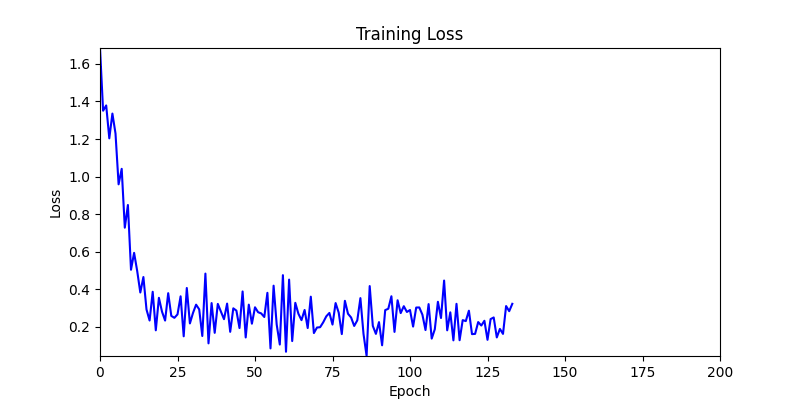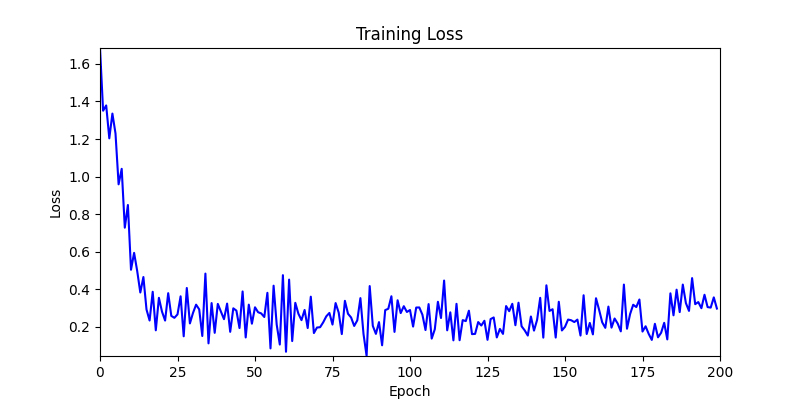
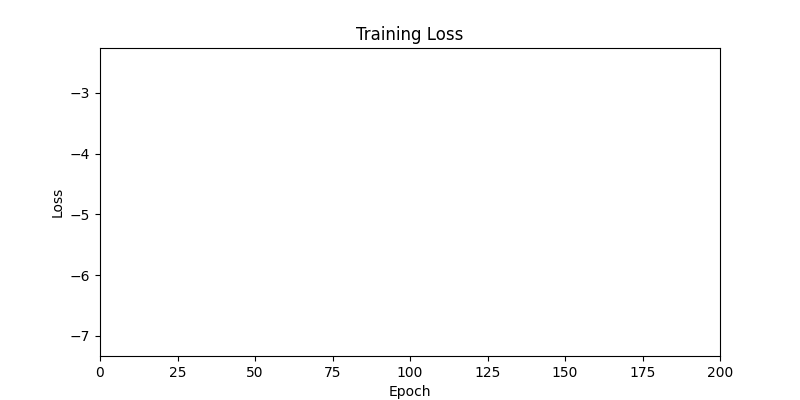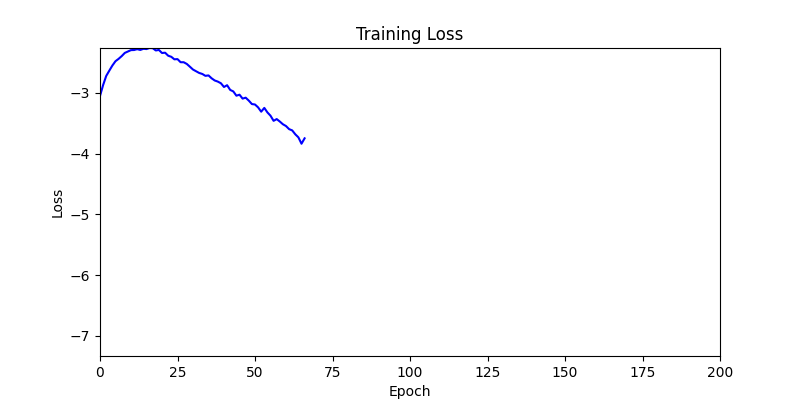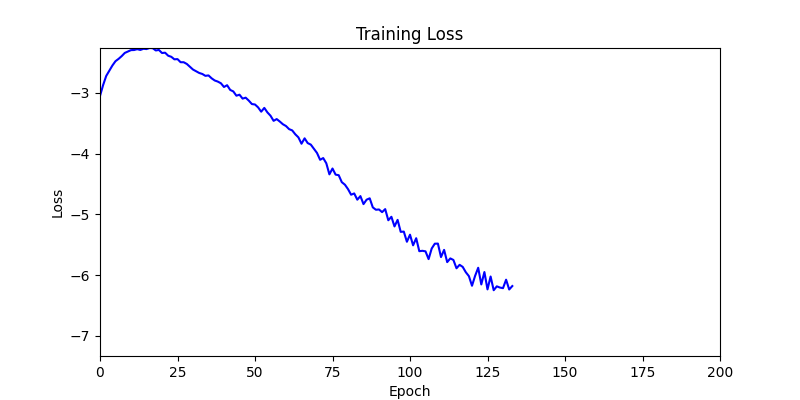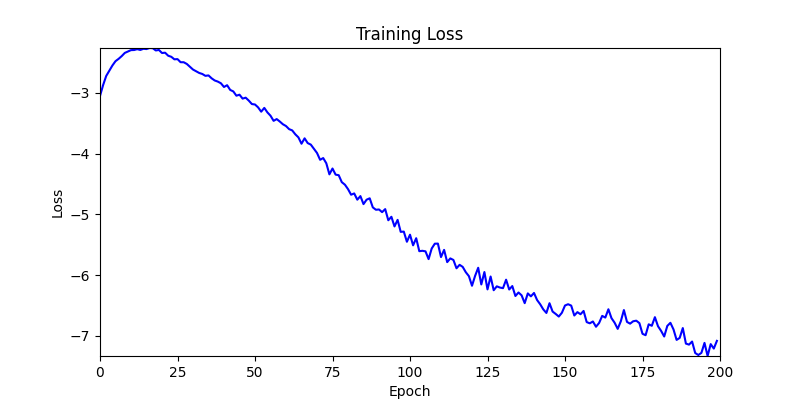
- 환경 2
Loss 1
Loss 2
Loss 3
Loss 4
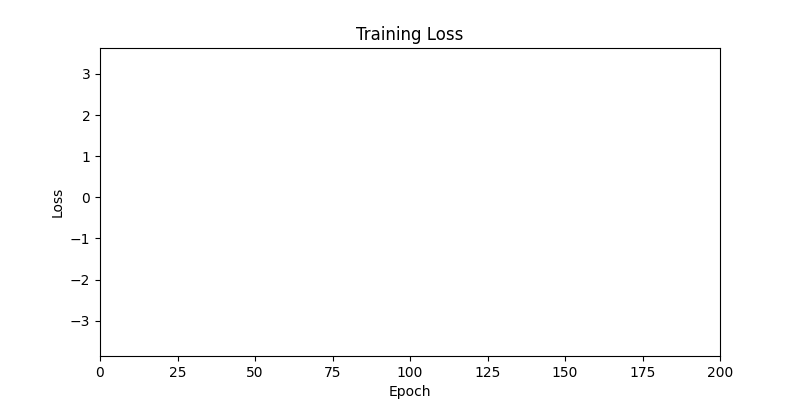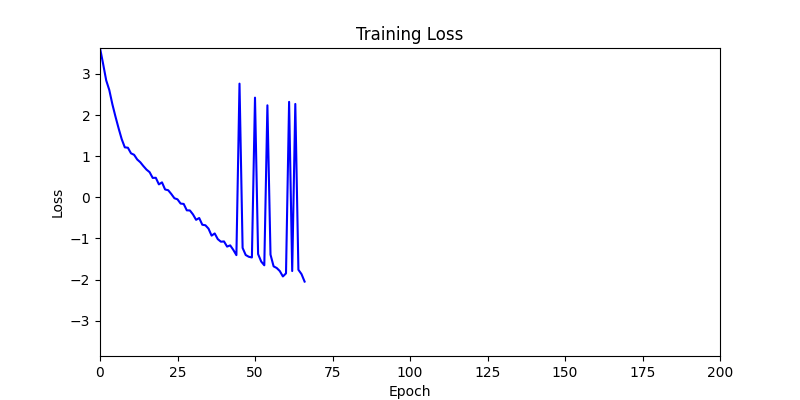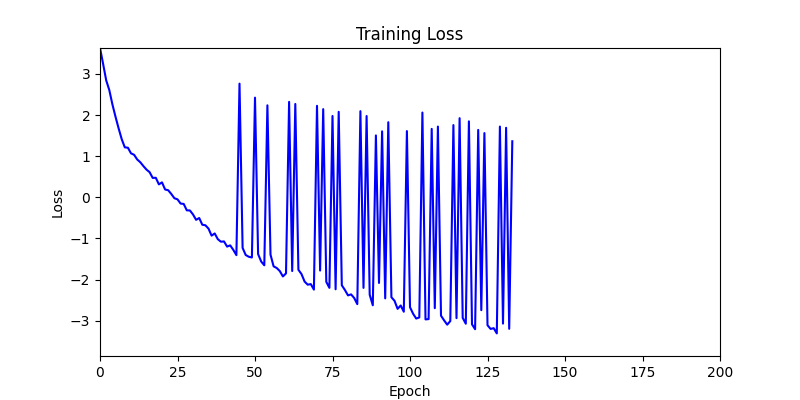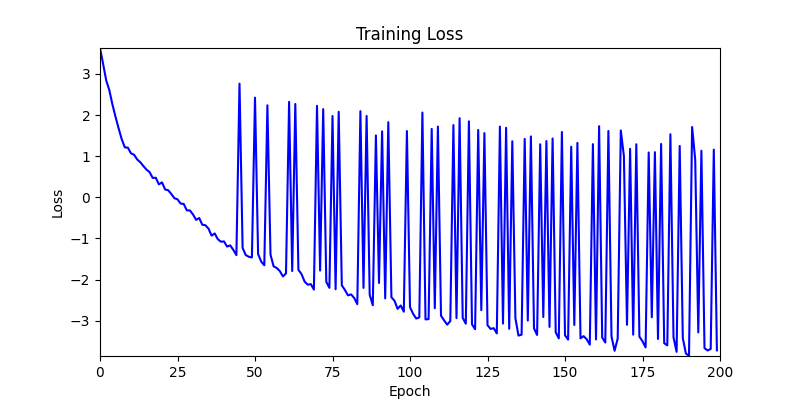
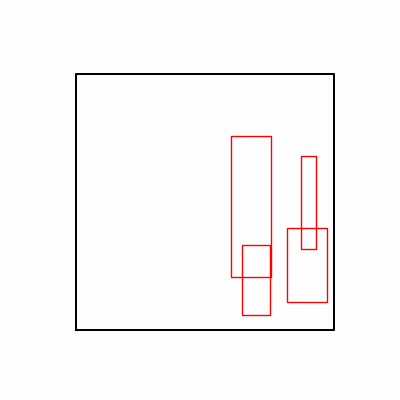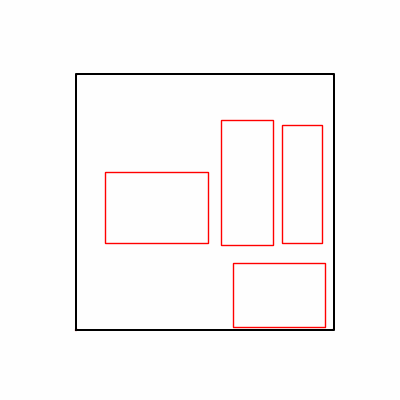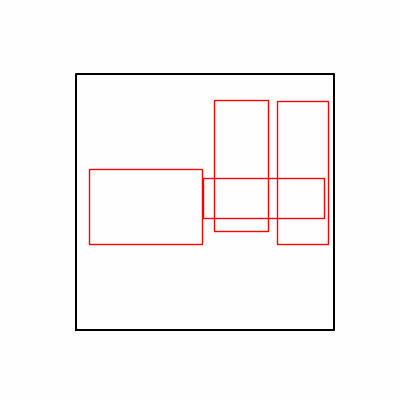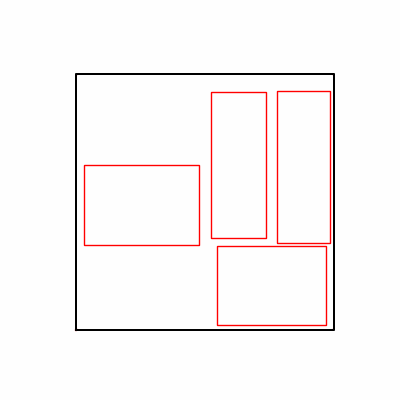
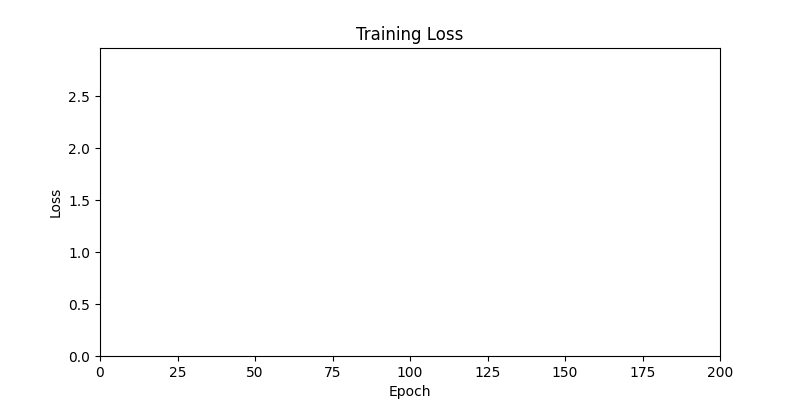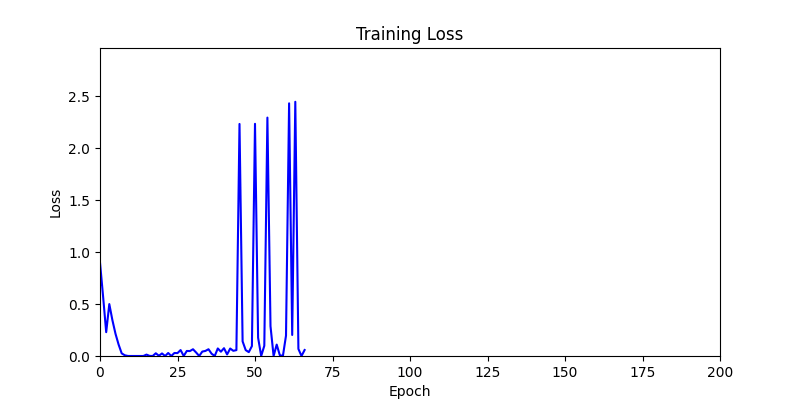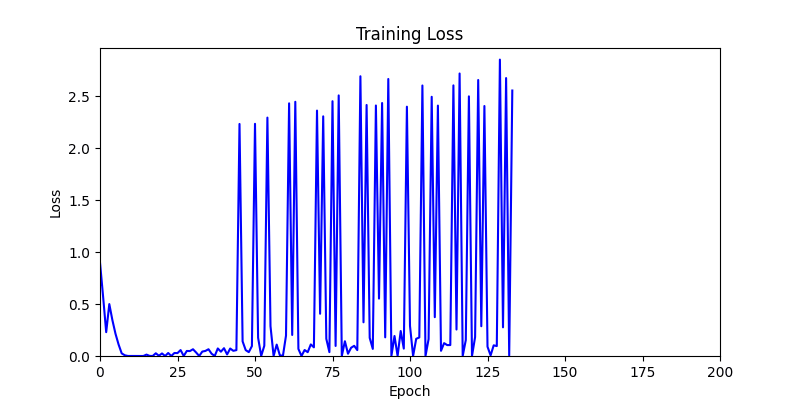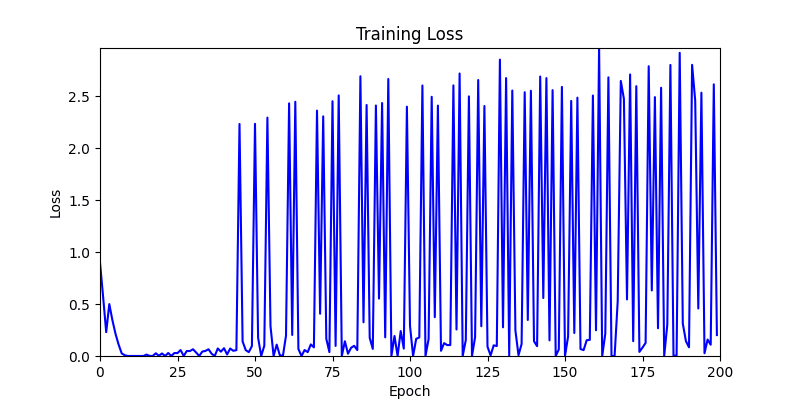
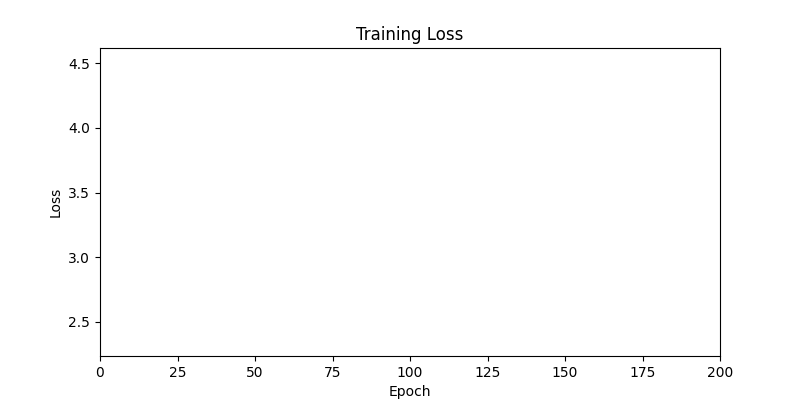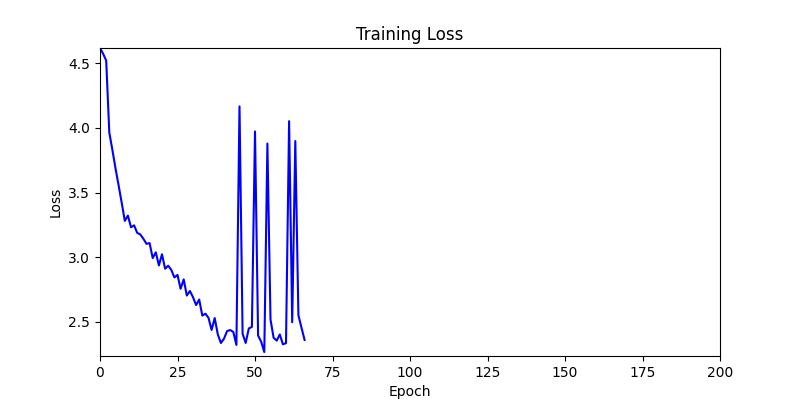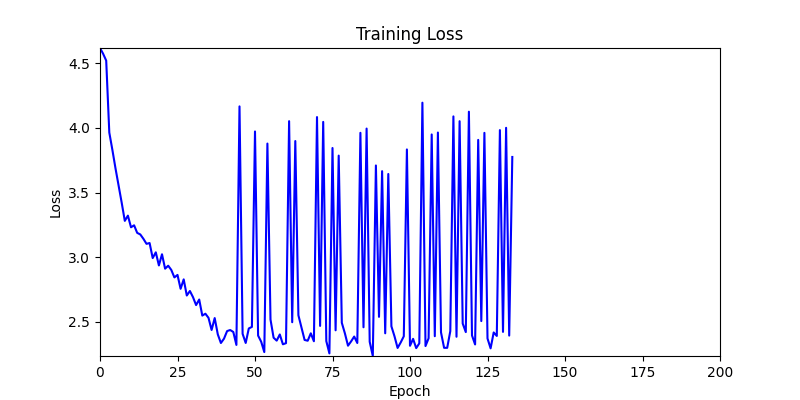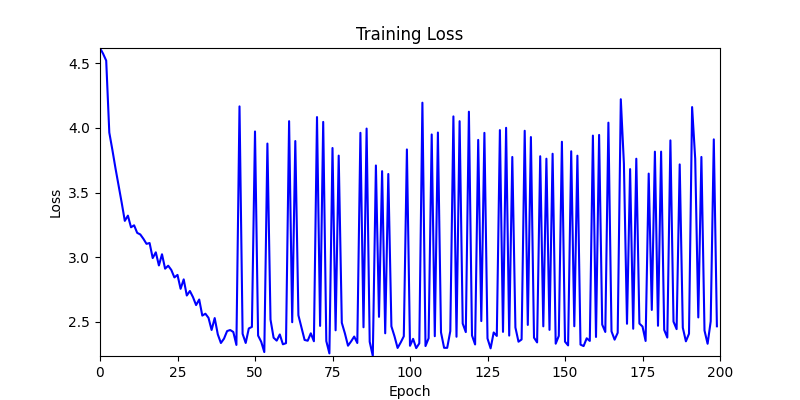
- 이제 이 두 환경을 이용해 ga 모듈 및 AdamW optimizer 를 이용한 최적화를 진행해보겠습니다.
1. AdamW Optimizer 를 이용한 최적화 Test results
optimizer = torch.optim.AdamW([parameters], lr=learning_rate)
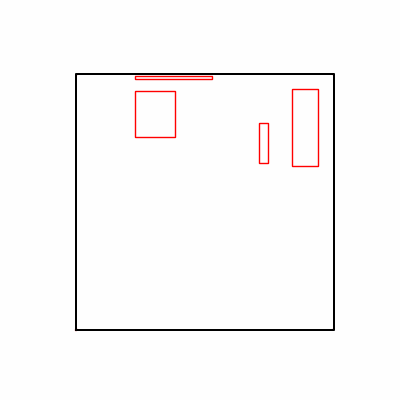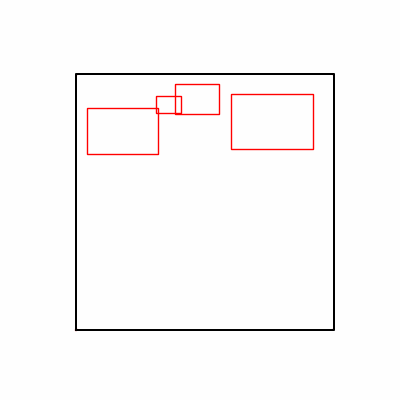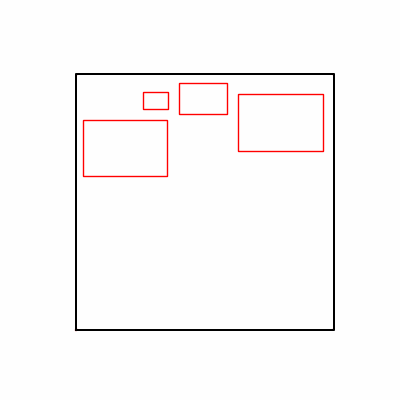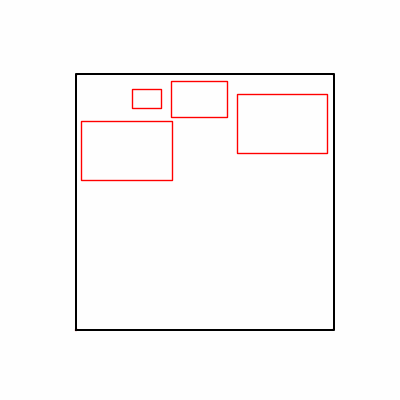
- 환경 1
Loss 1
Loss 2
Loss 3
Loss 4
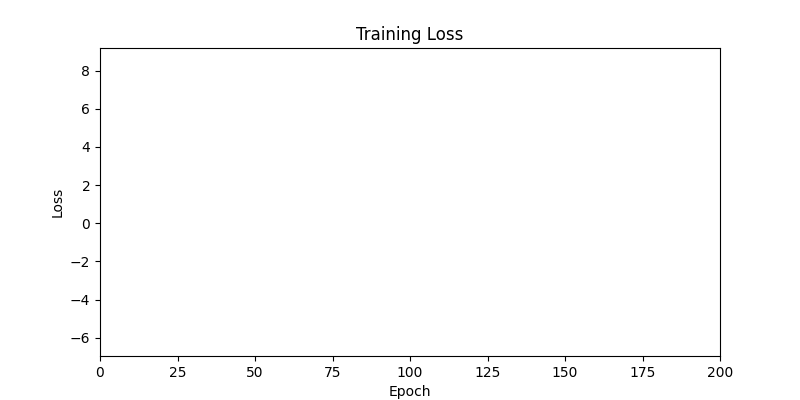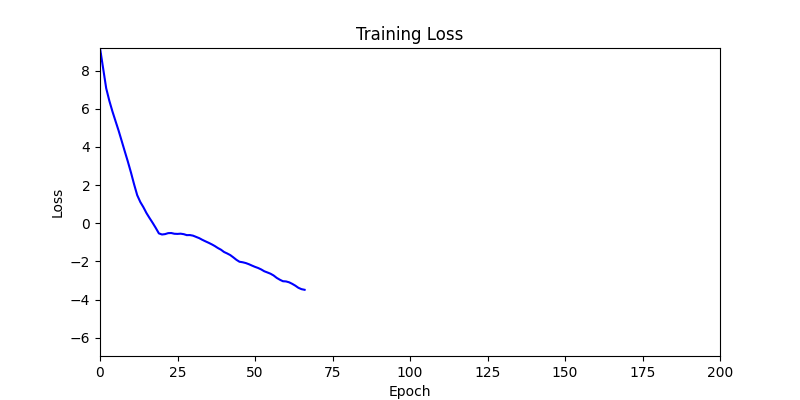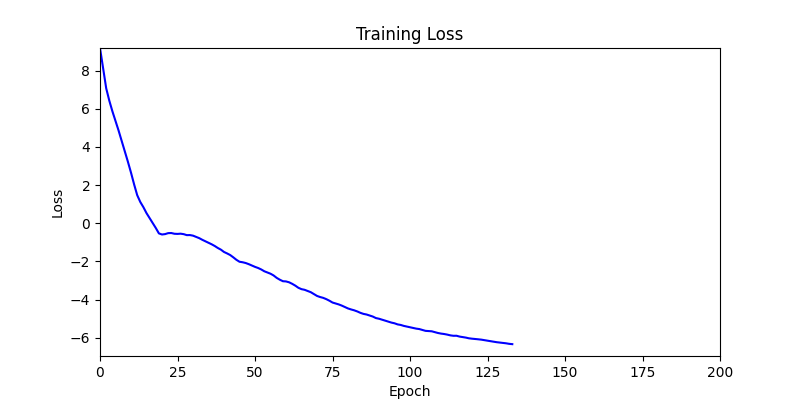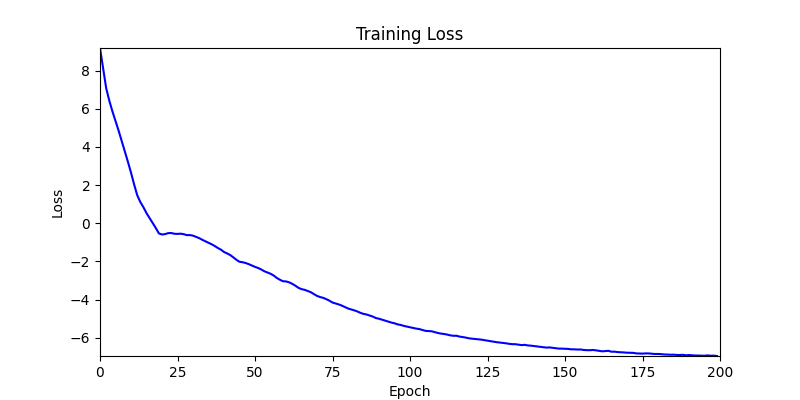
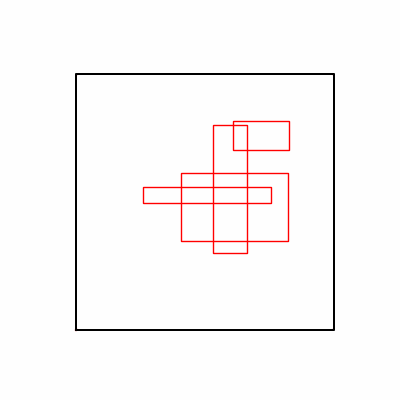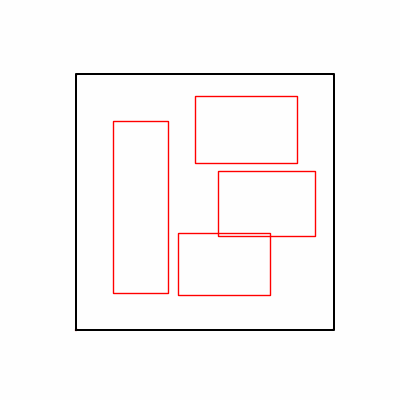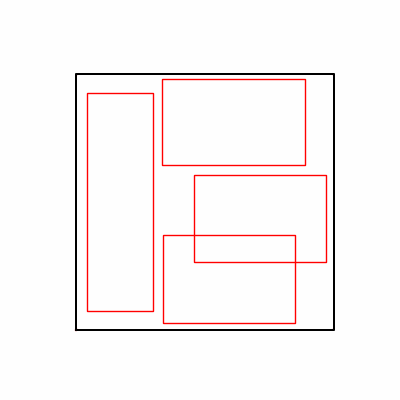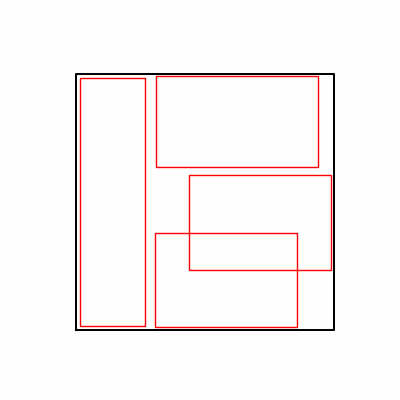
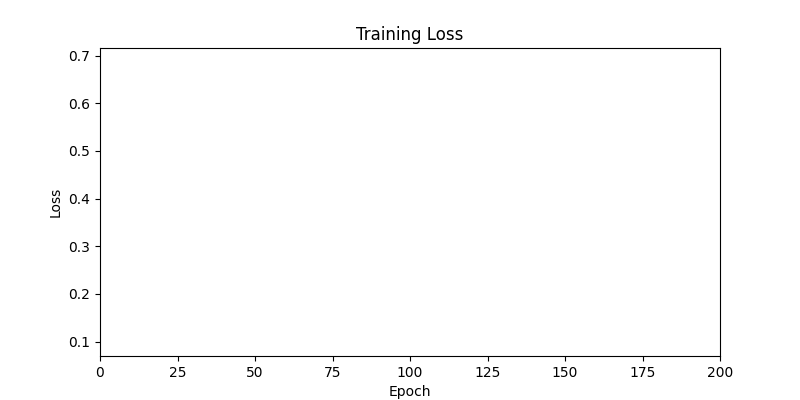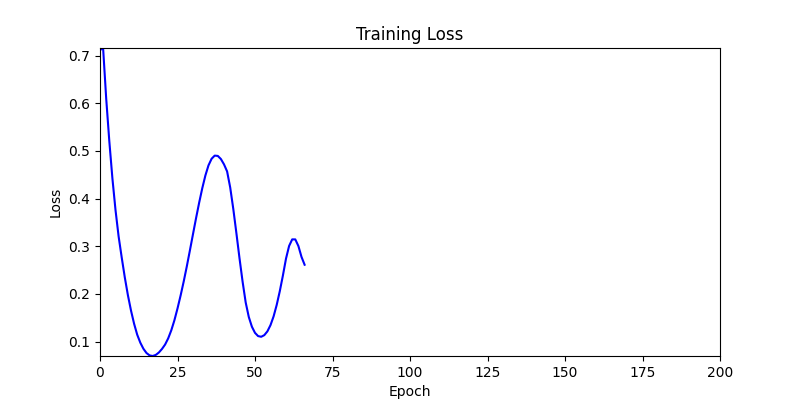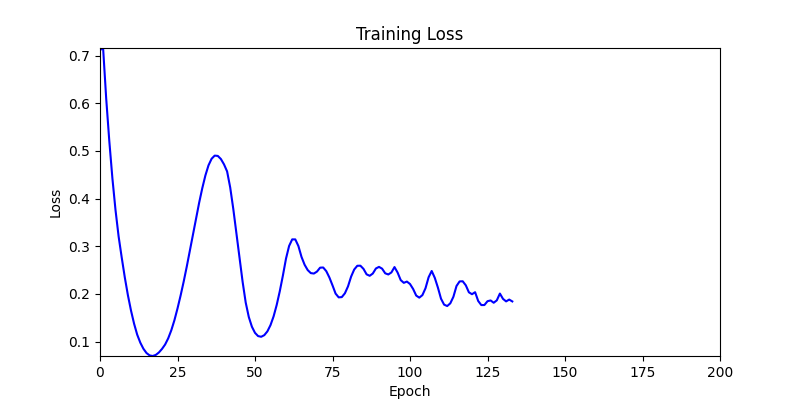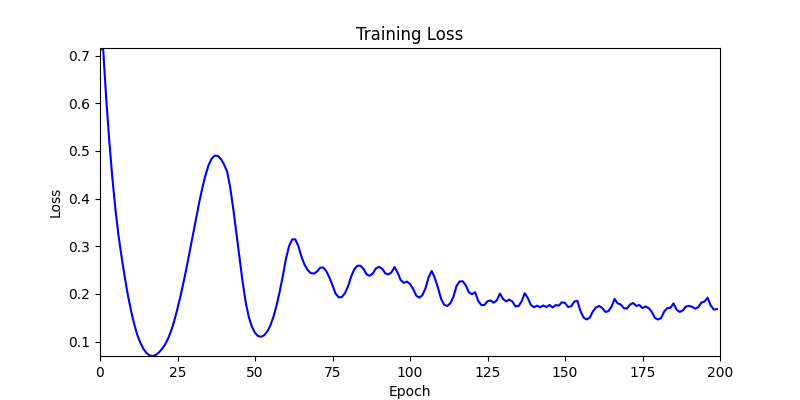
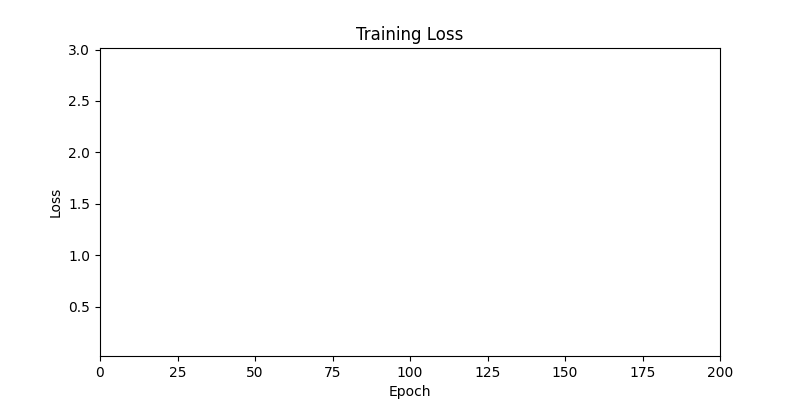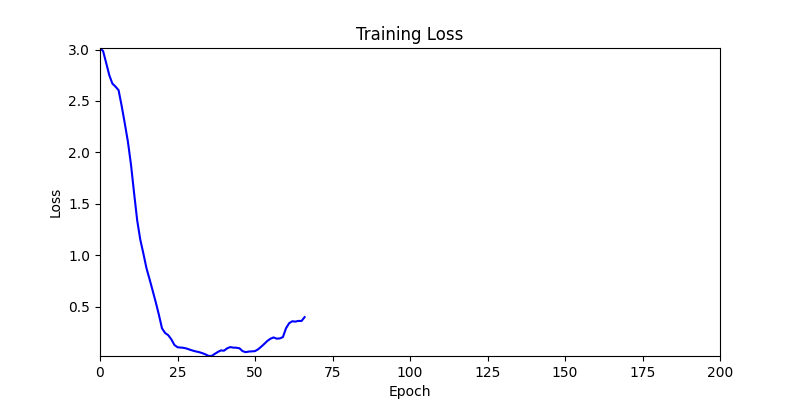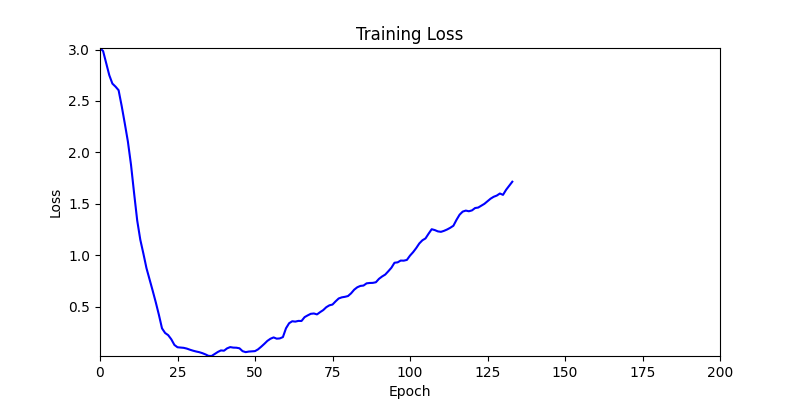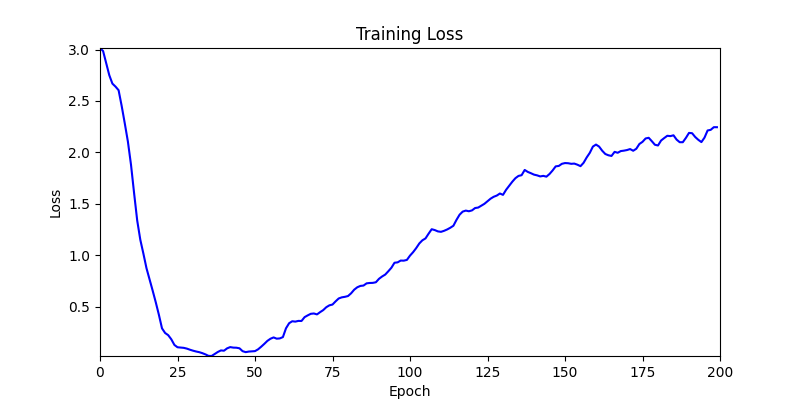
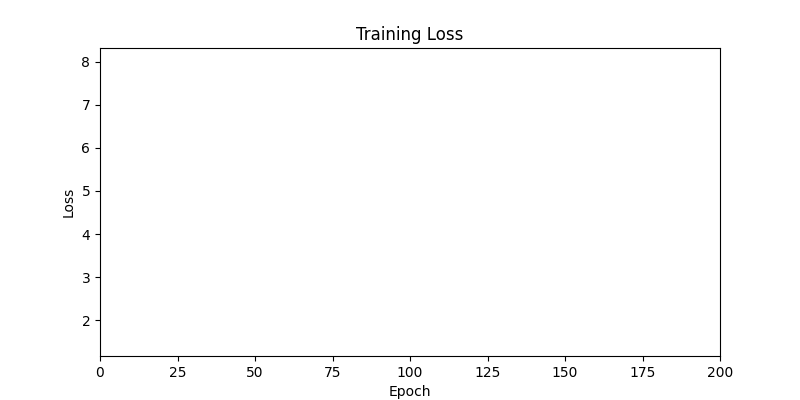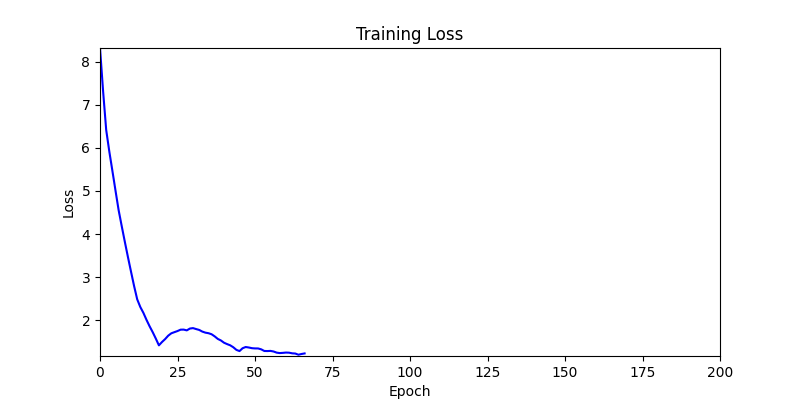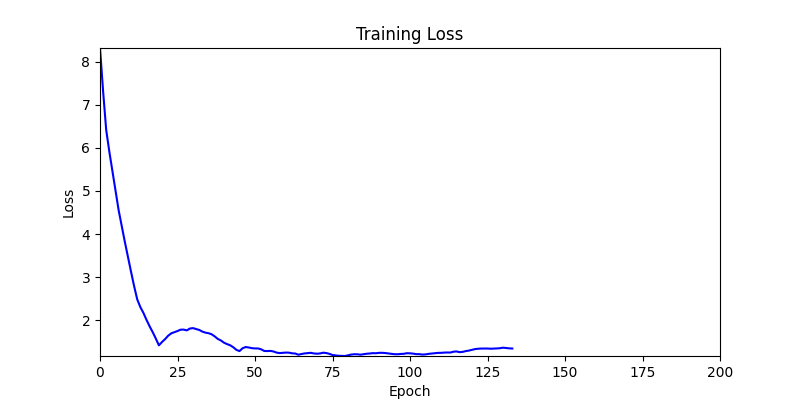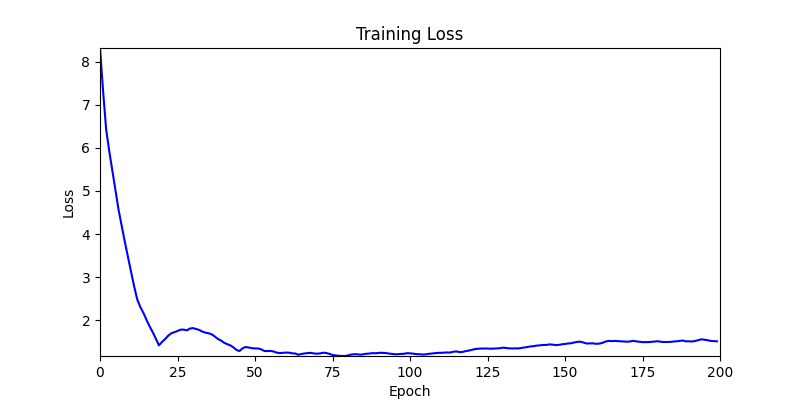
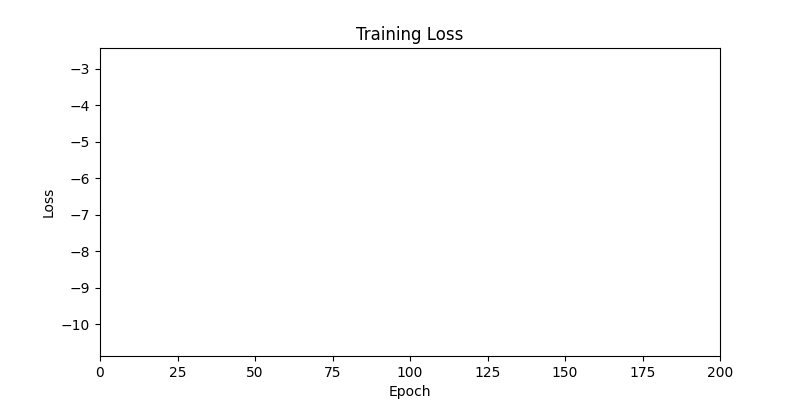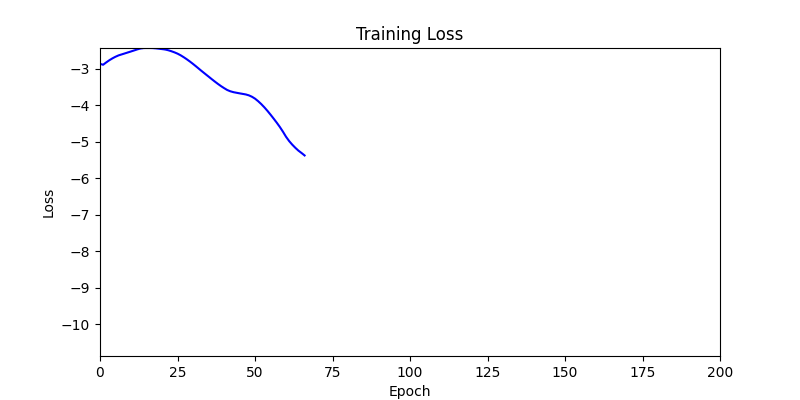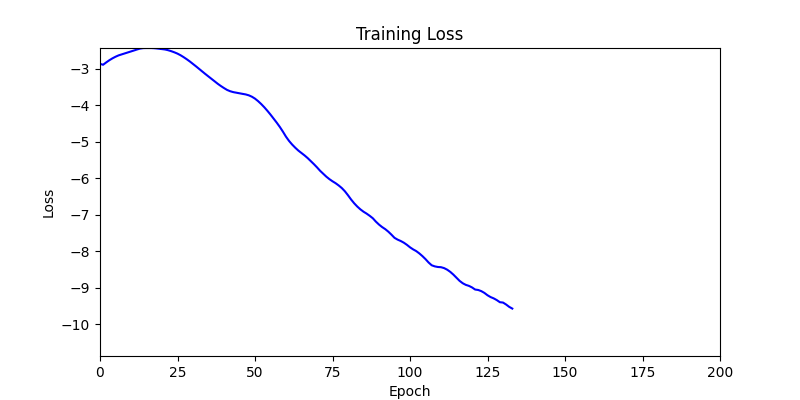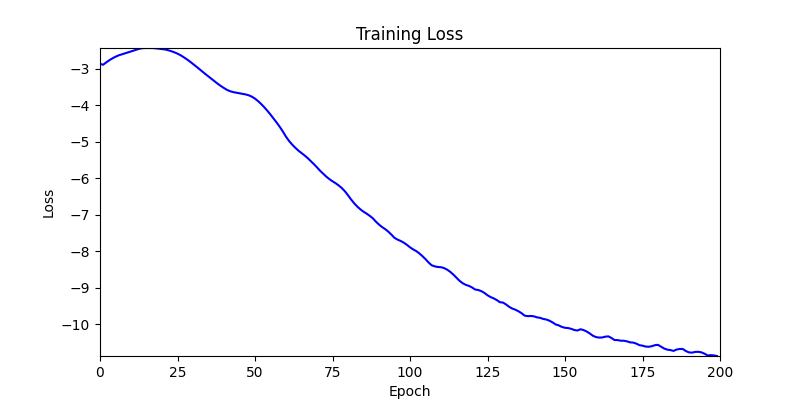
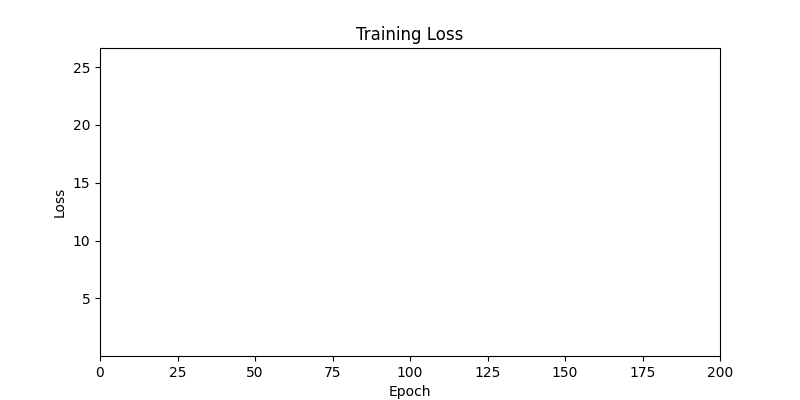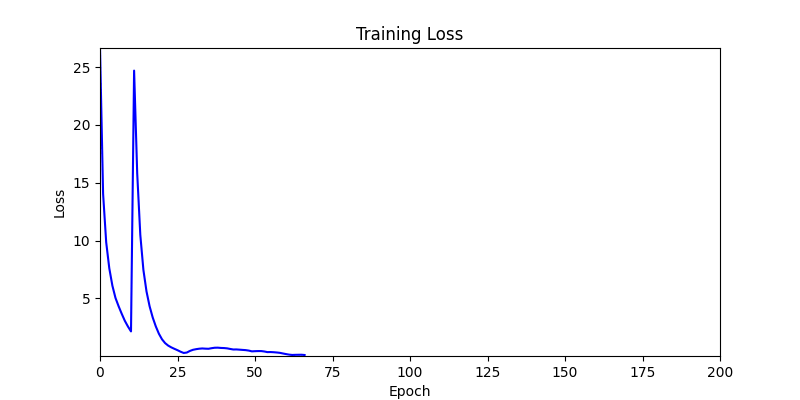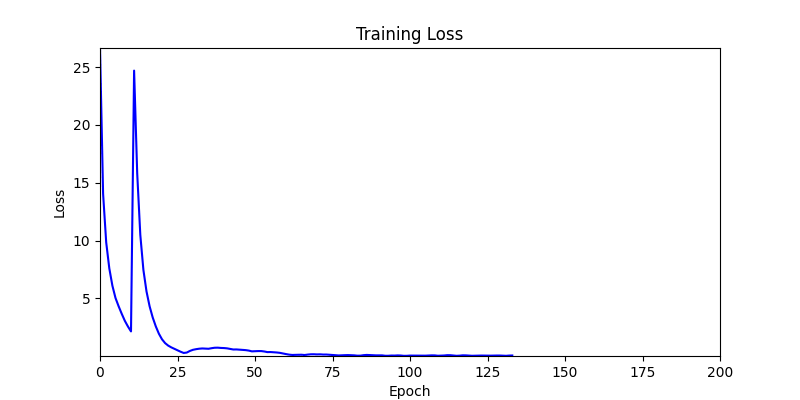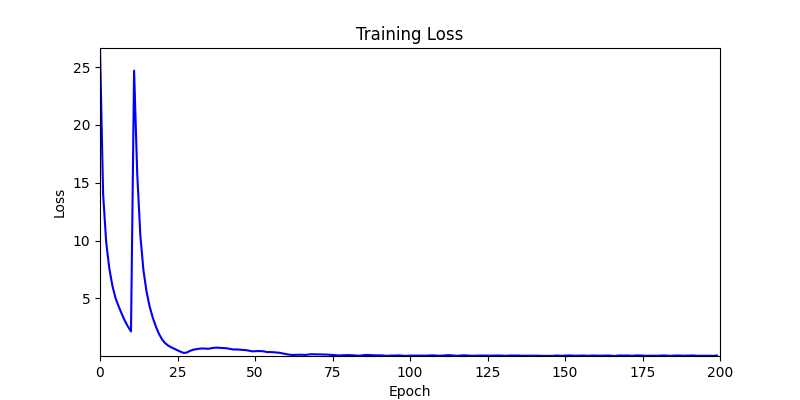
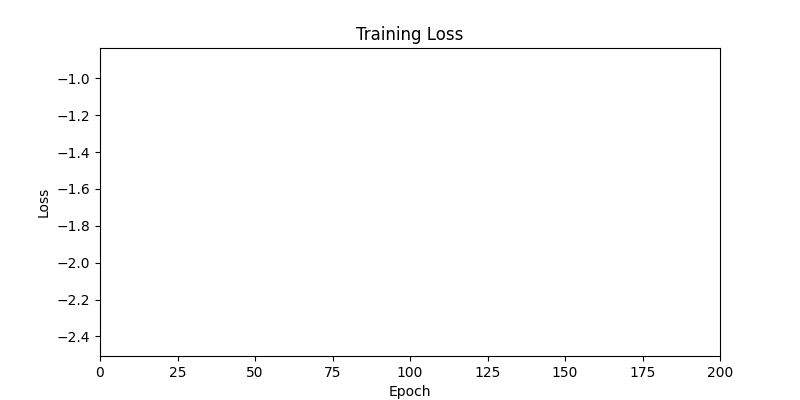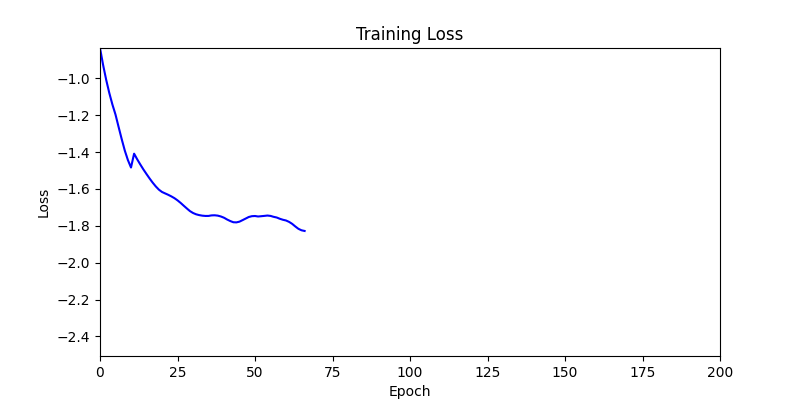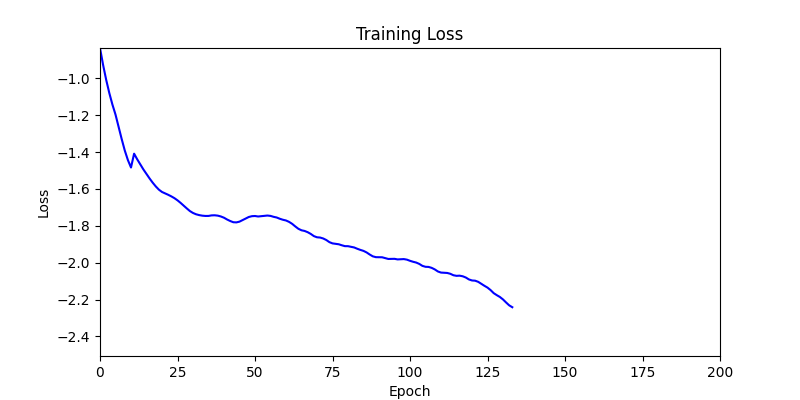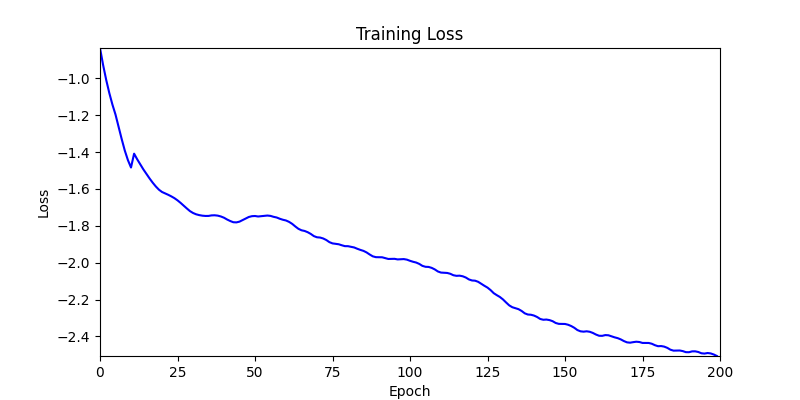
- 환경 2
Loss 1
Loss 2
Loss 3
Loss 4
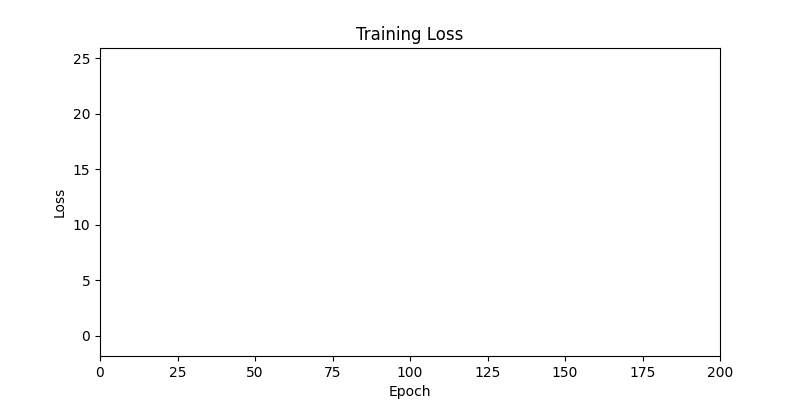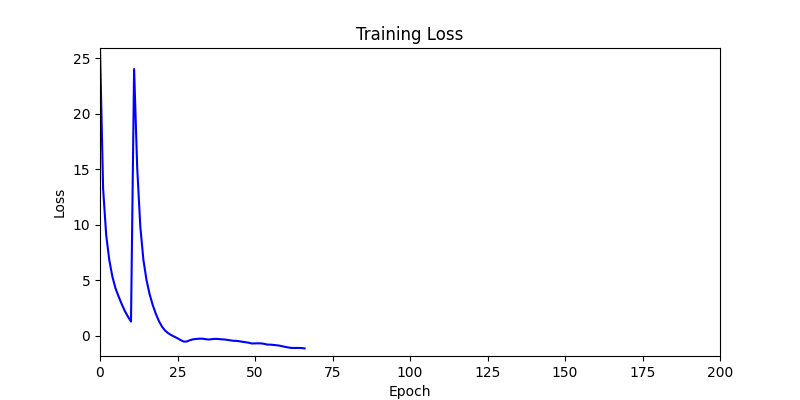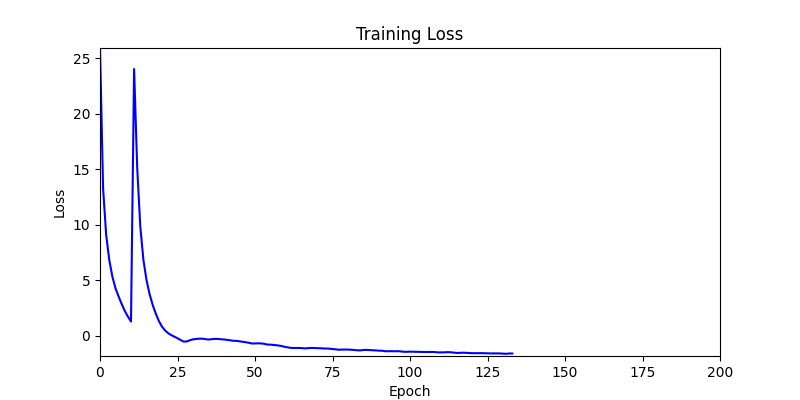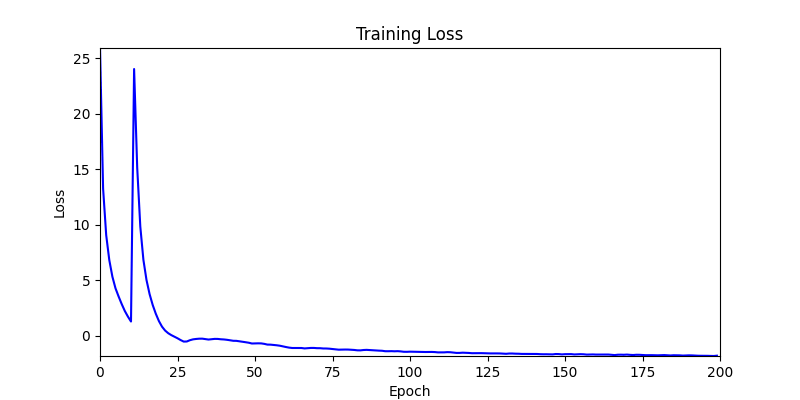
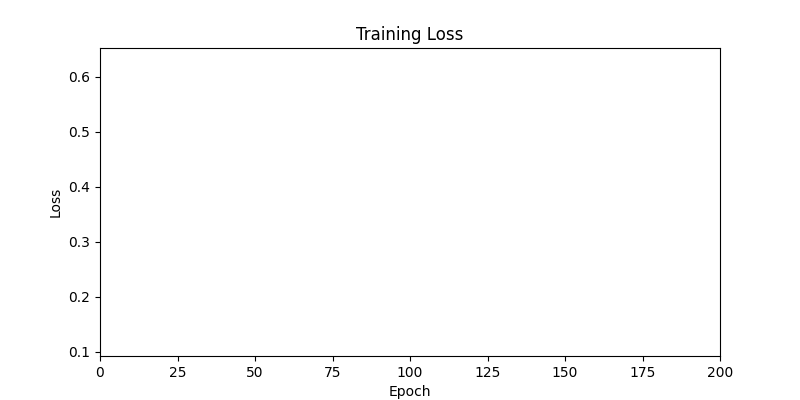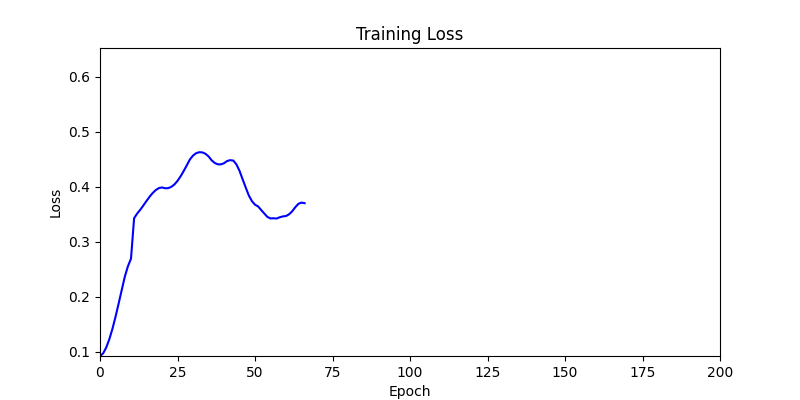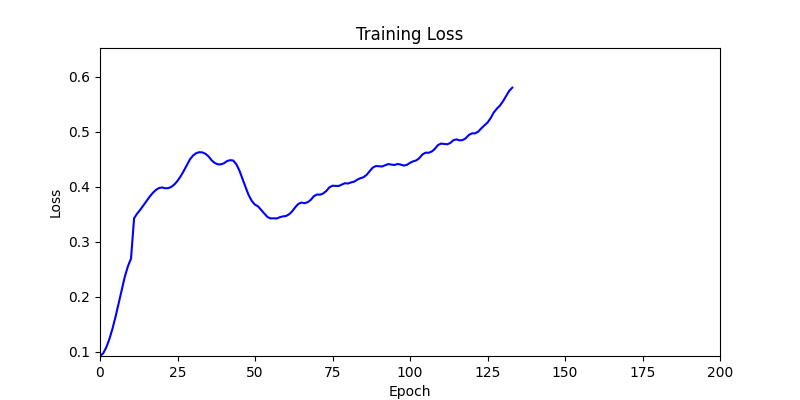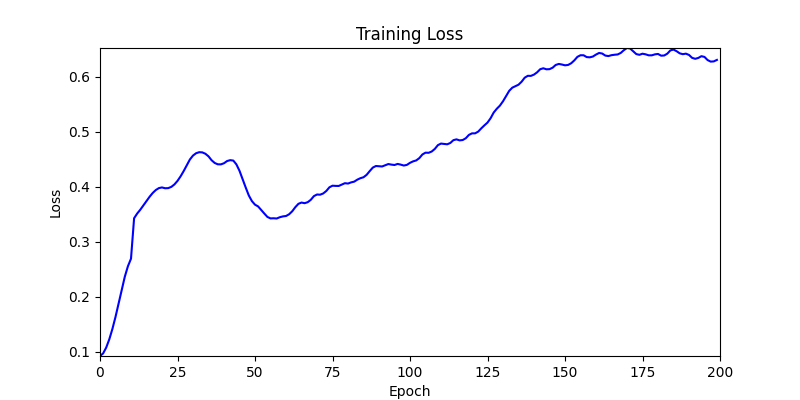
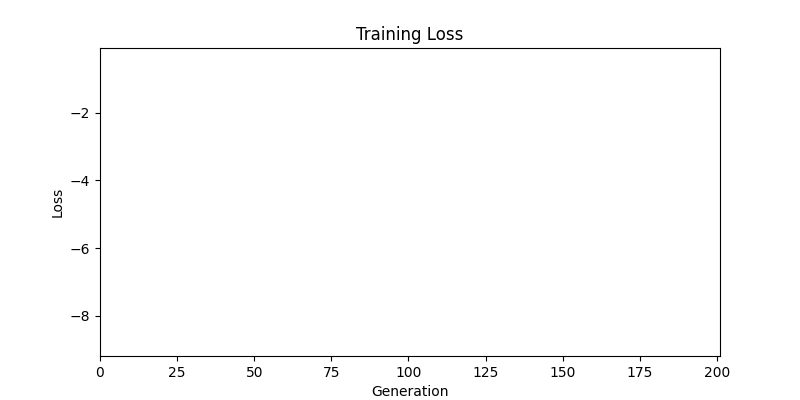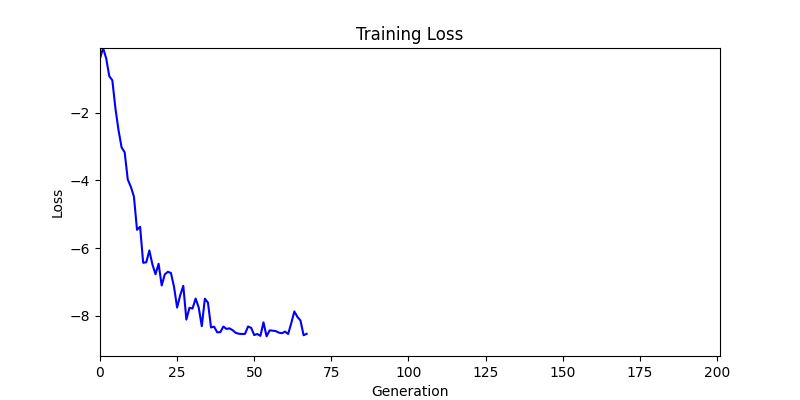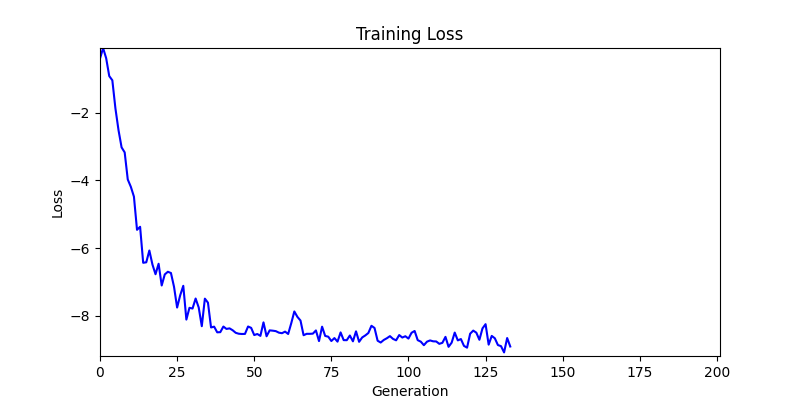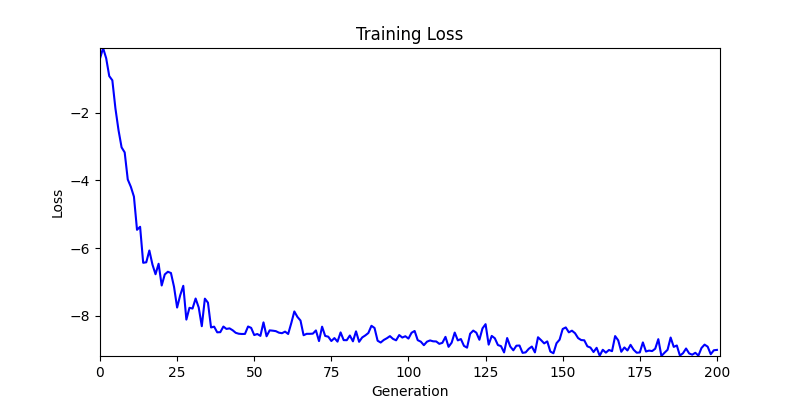
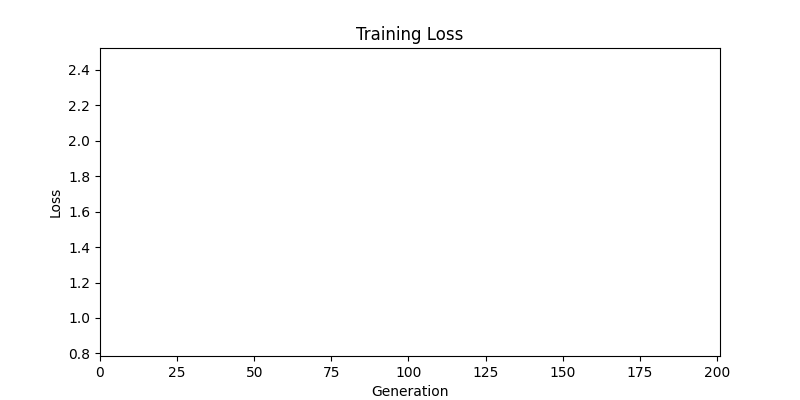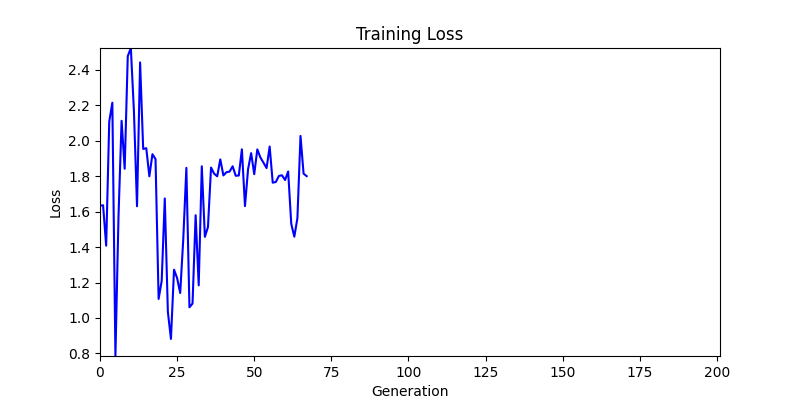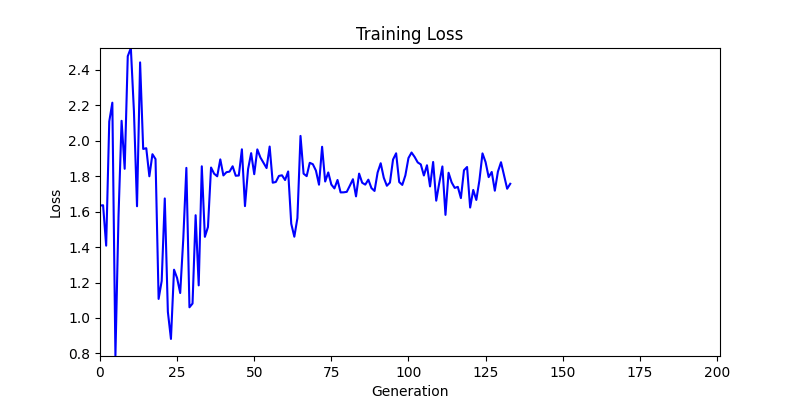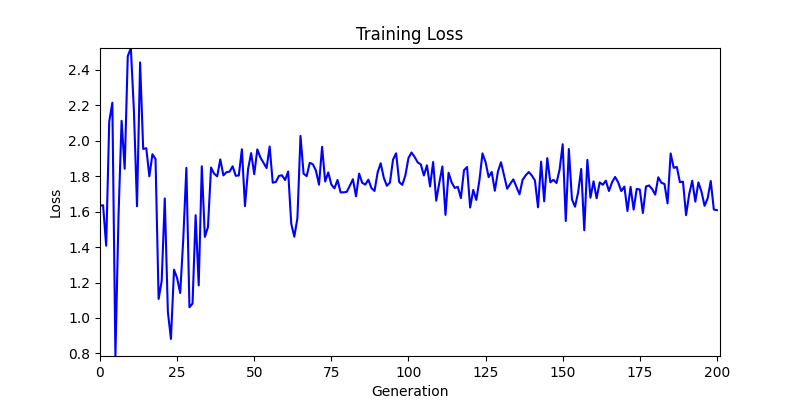
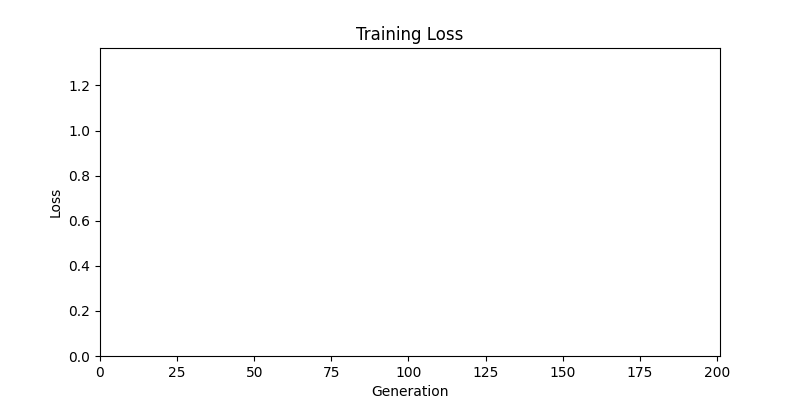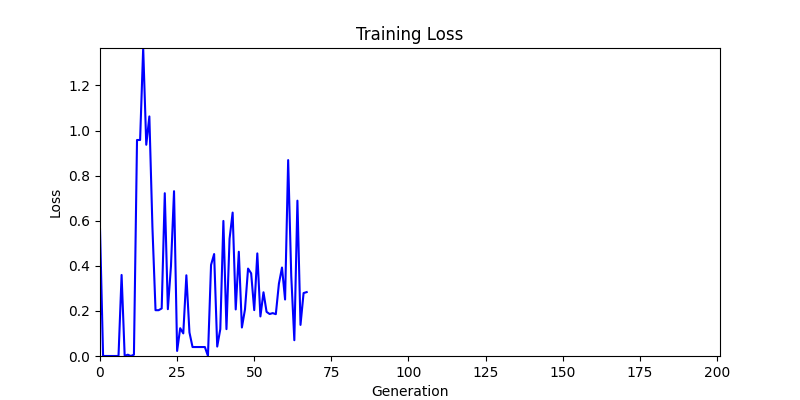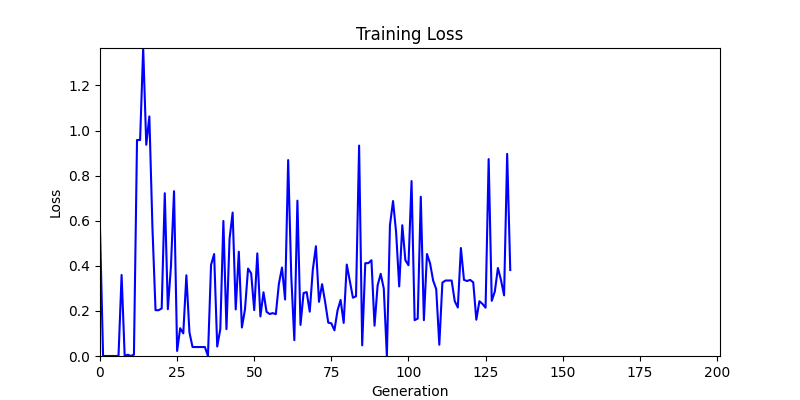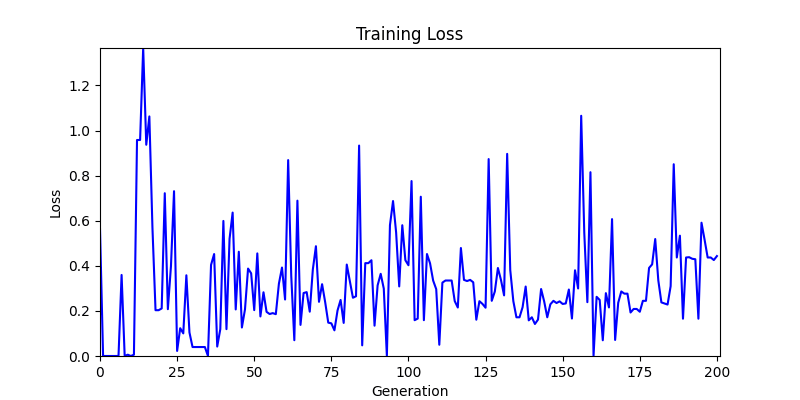
2. Genetic Algorithm 를 이용한 최적화 Test results
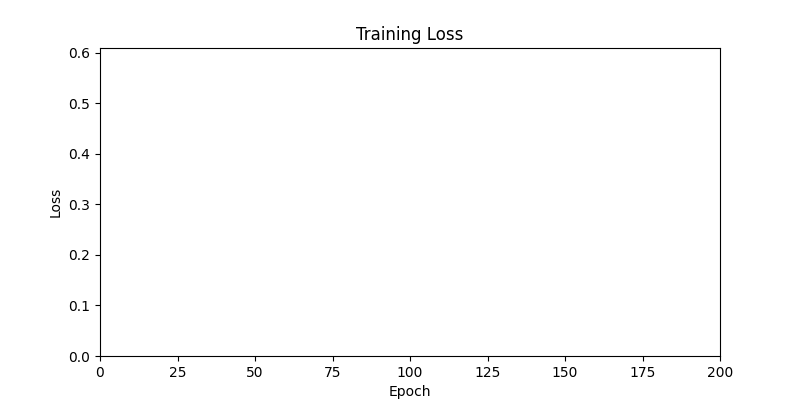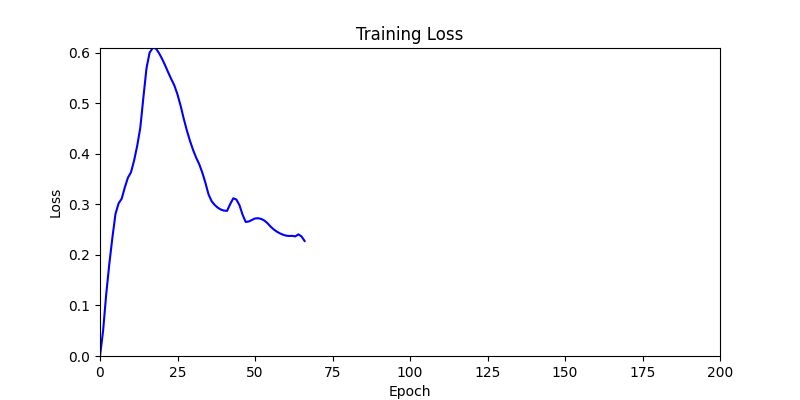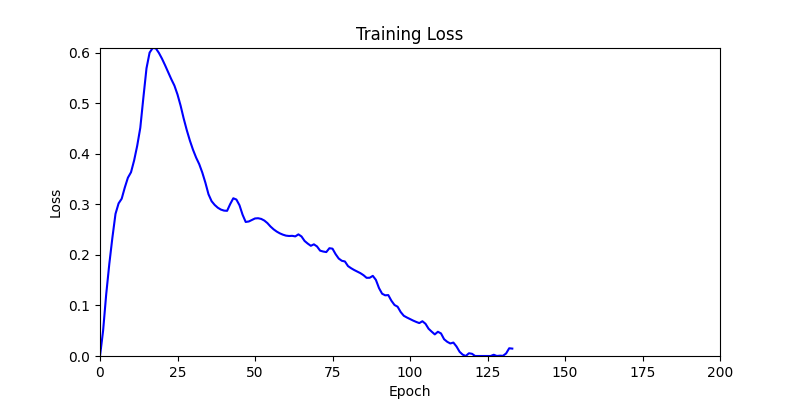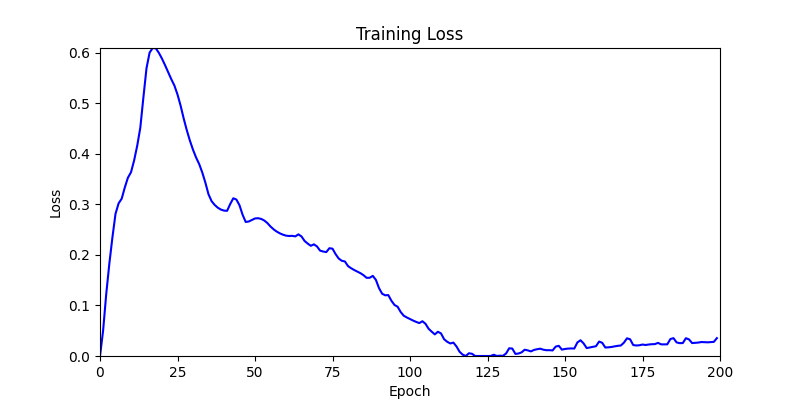
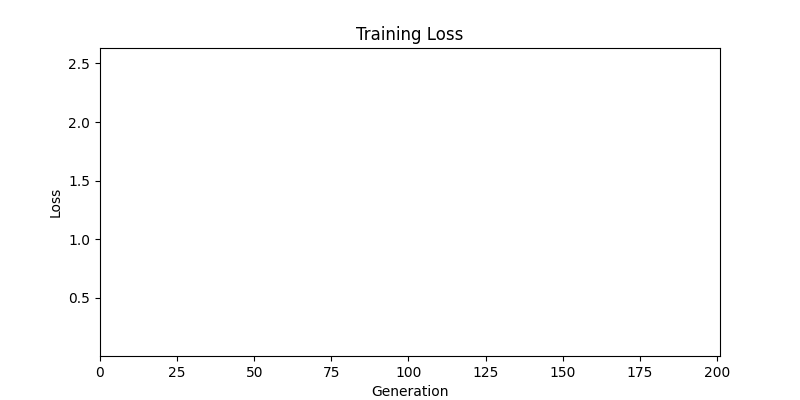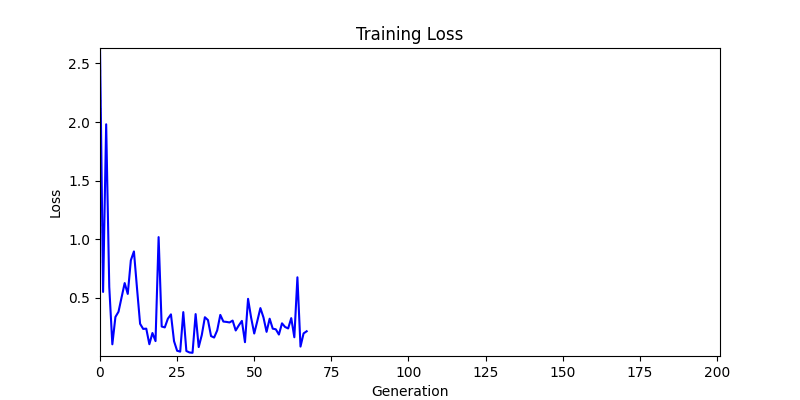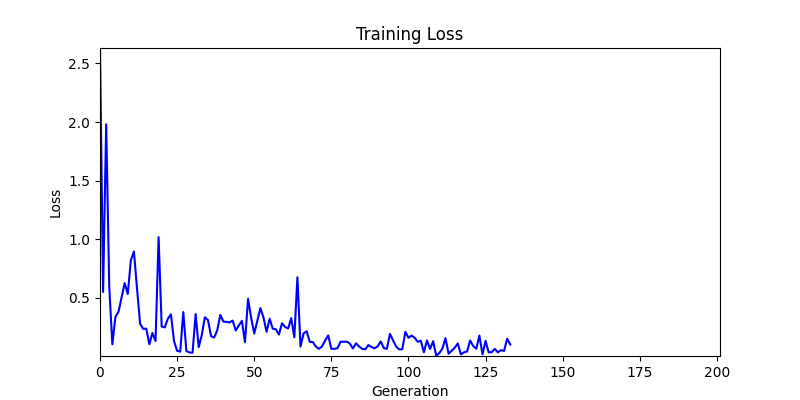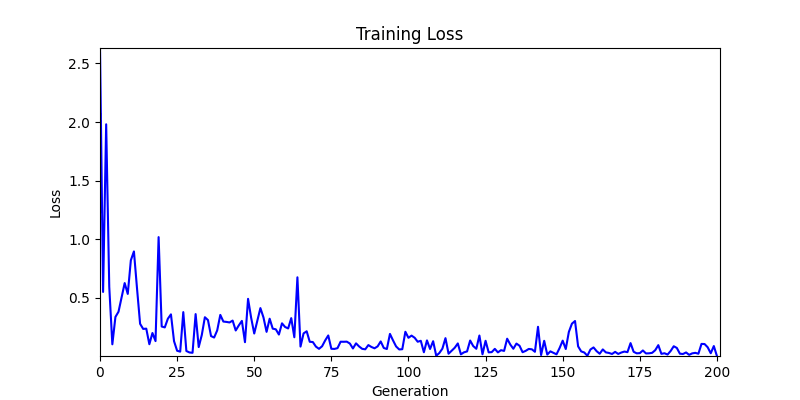
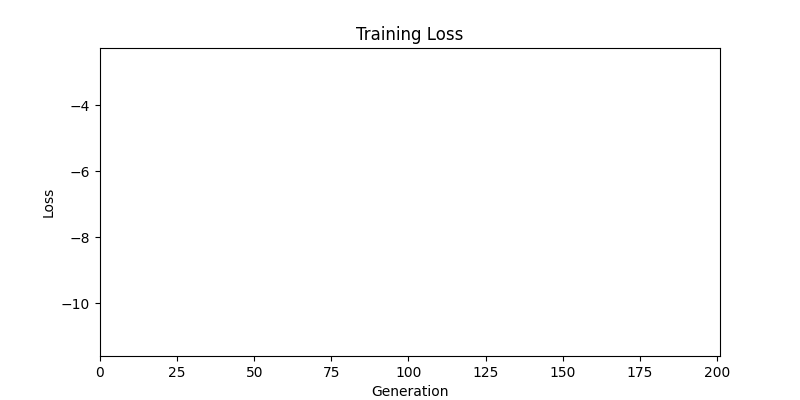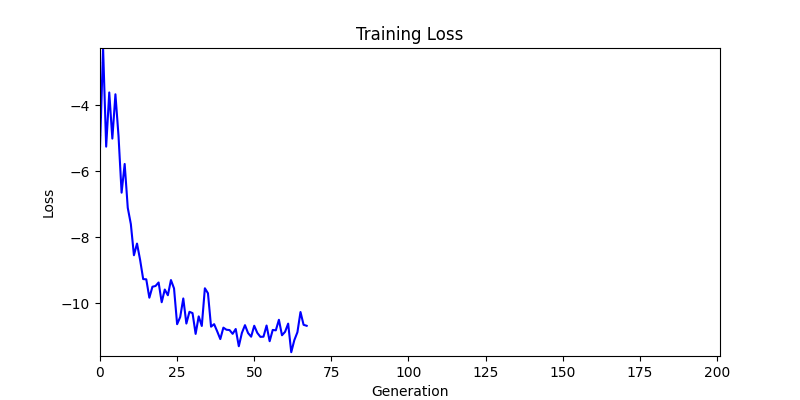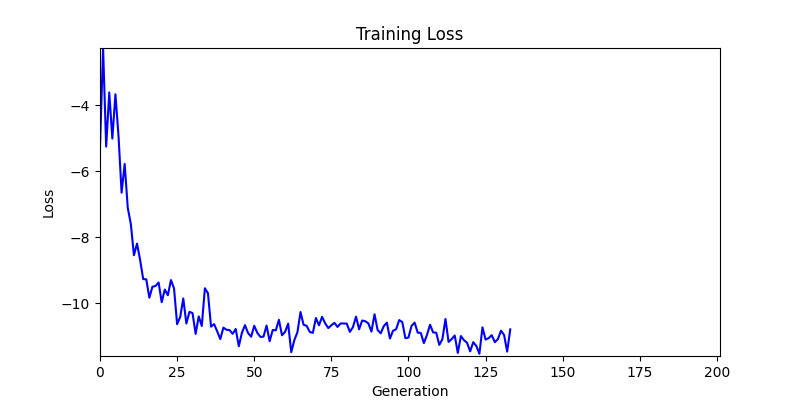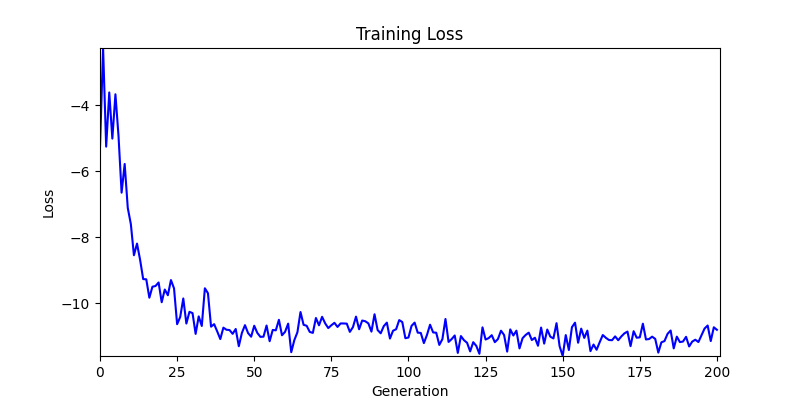
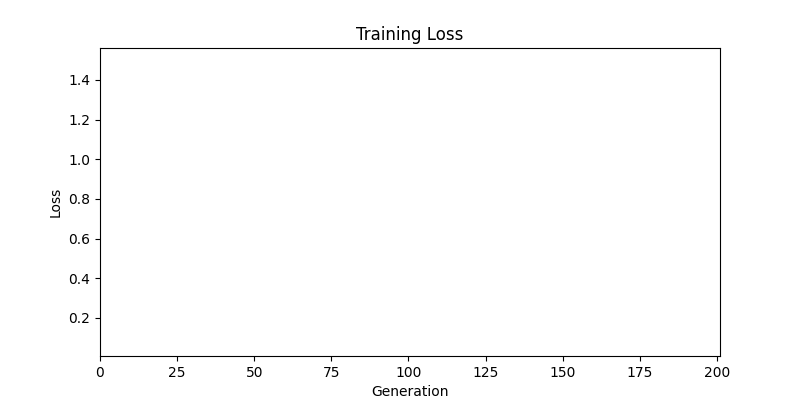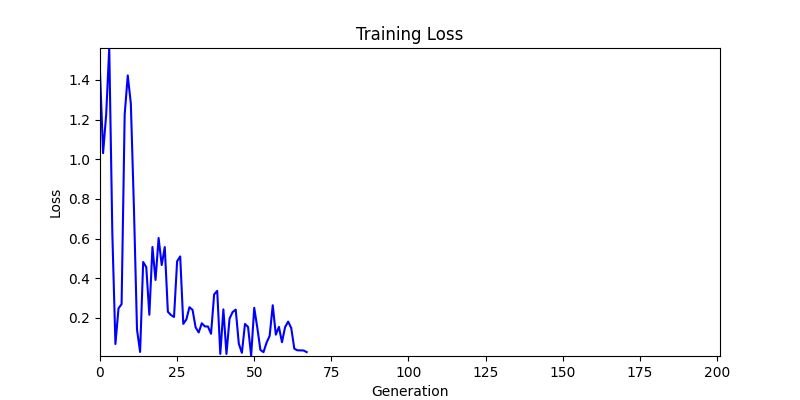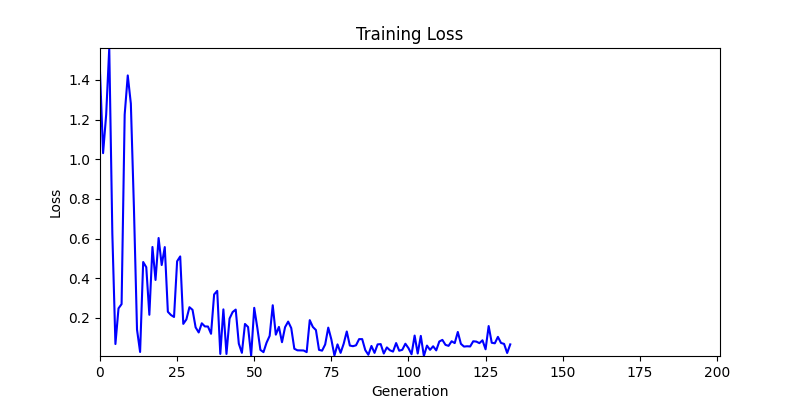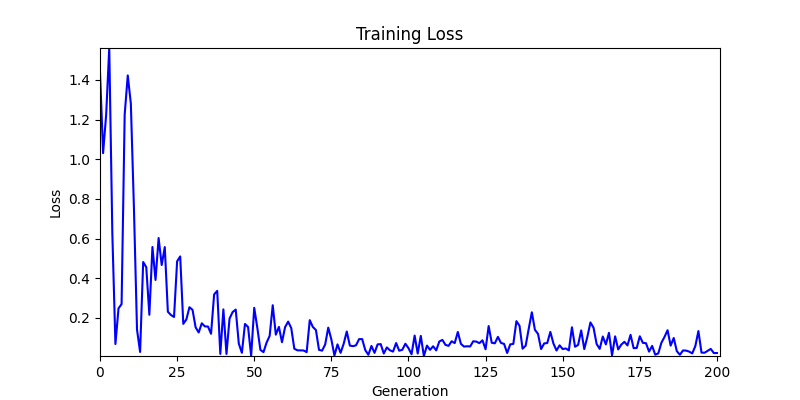
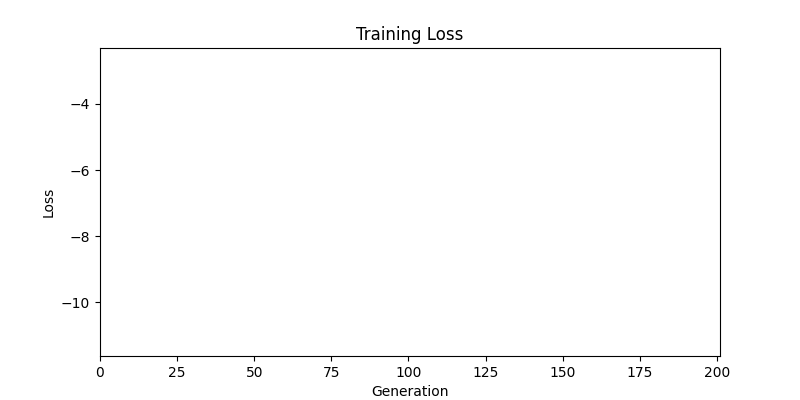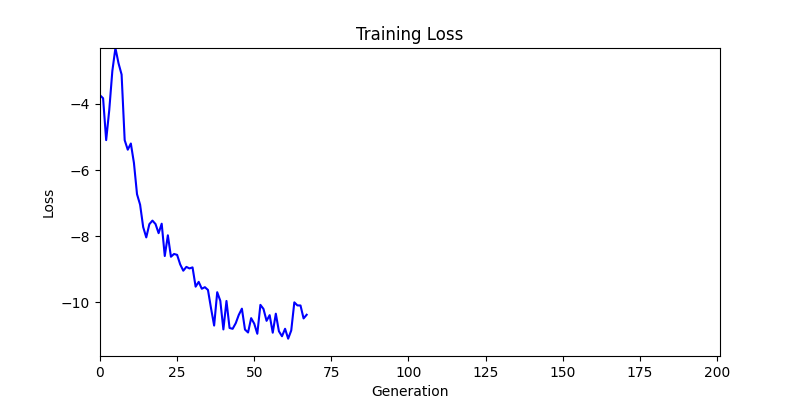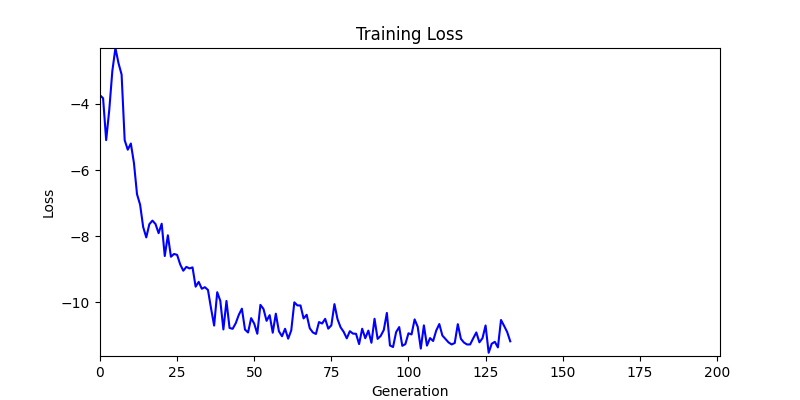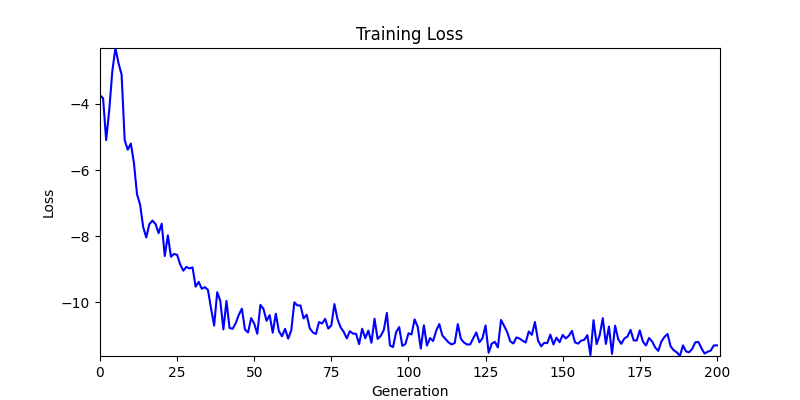
- ga 에서는 최종적인 결과는 유사하게 나오고 있습니다. 충분한 양의 연산이 주어지면, 탐색 영역 자체는 동일하기 때문에 거의 동일한 점수로 수렴하는 것을 확인할 수 있습니다.
- 하지만 연산을 매번 충분히 주어지는 것은 불가능 하는 경우가 많습니다. 최대한 답을 향해 빨리 나아가는 것 역시 중요합니다. 환경 1이 확실히 초기 안정성이 더 좋은 것 역시 확인이 가능합니다.
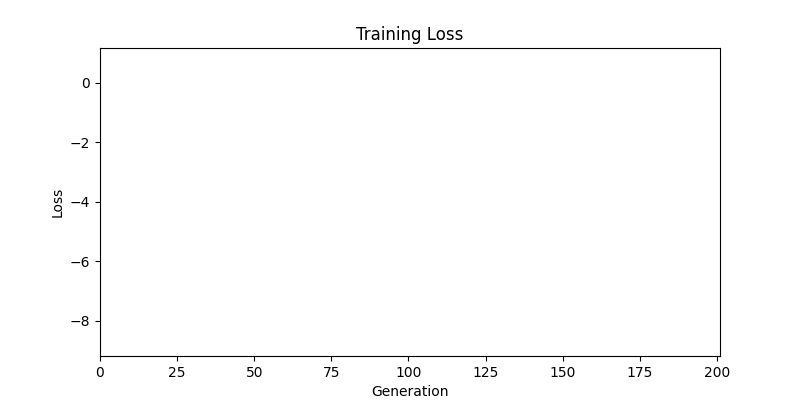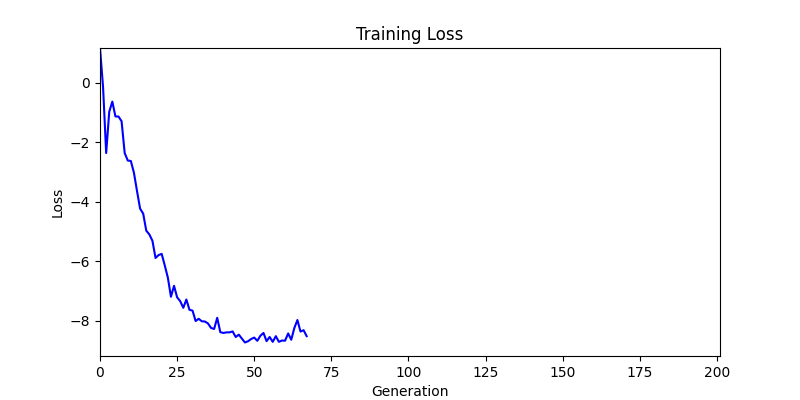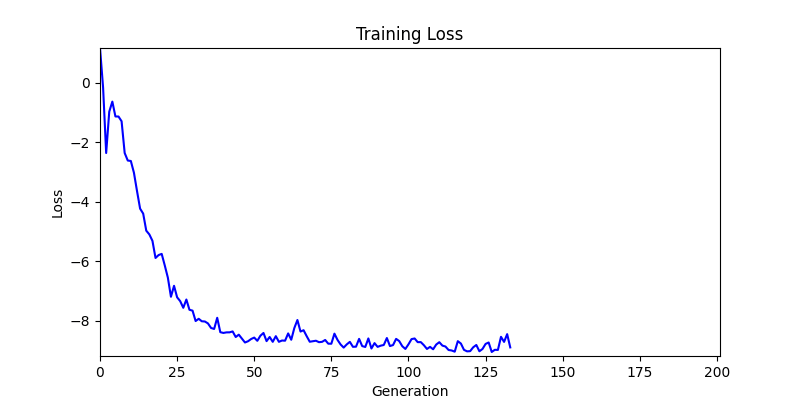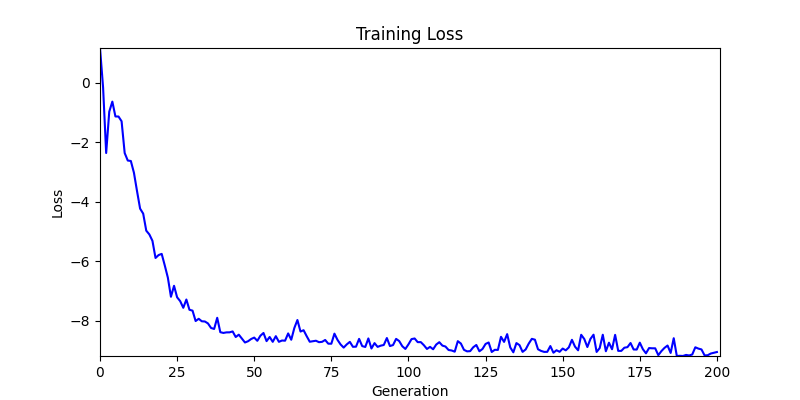
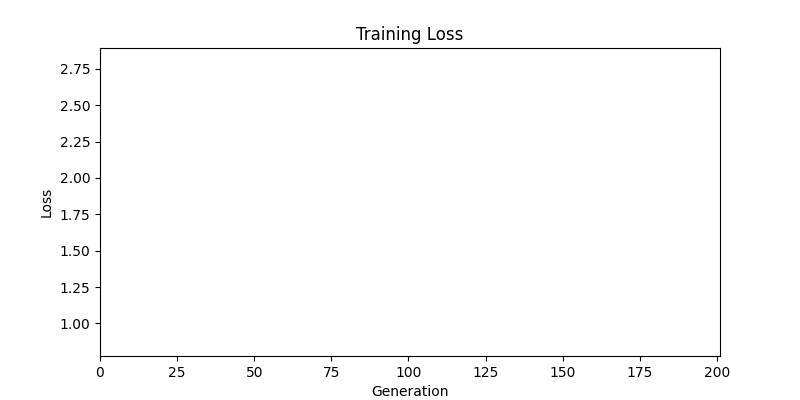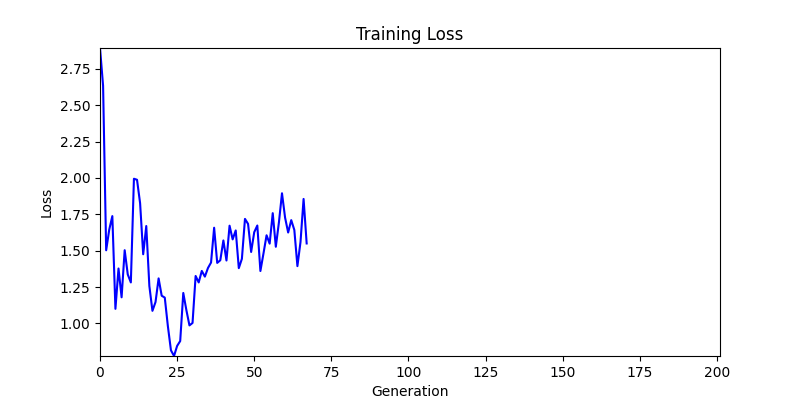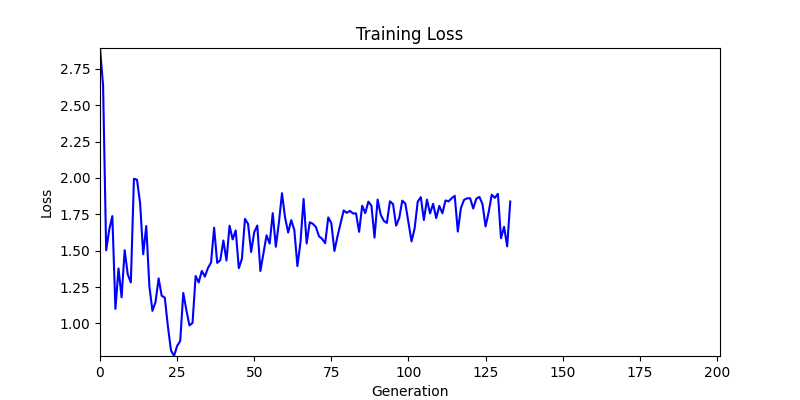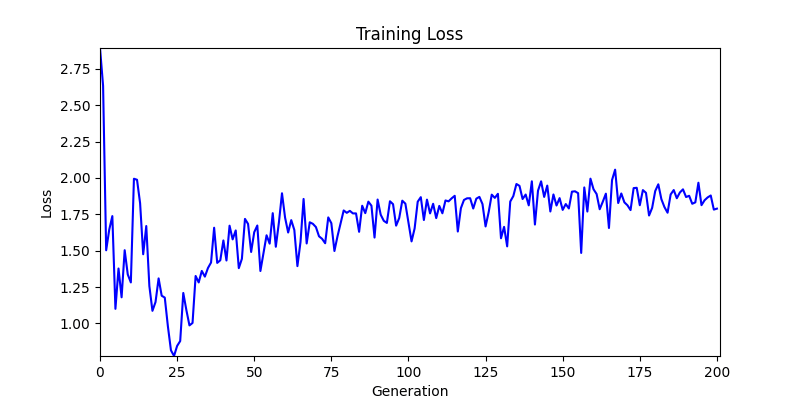
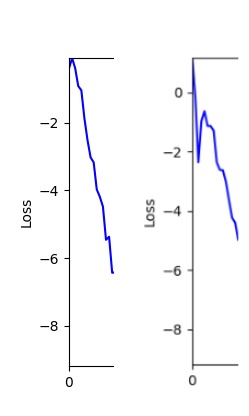두 환경의 초기 그래프 차이 - 더욱이 ga 에서는 generation 당 100개의 Population 을 사용했습니다. 즉, 200 번의 연산만 수행했던 위 두 케이스와 다르게 20000번의 연산을 수행한 결과입니다. ga 를 사용하는 것이 최종적인 성능을 보장하는 방법 중에 하나일 수는 있지만, 적어도 이 셋중에는 효율적인 방식이라 보기 어렵습니다. (단 2 generation 만에 200번의 연산)
- 환경 1
Loss 1
Loss 2
Loss 3
Loss 4
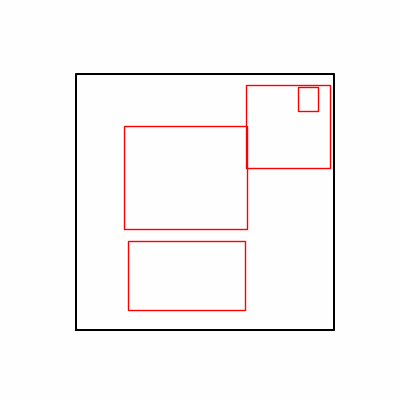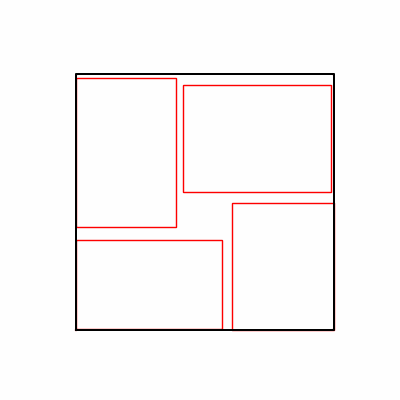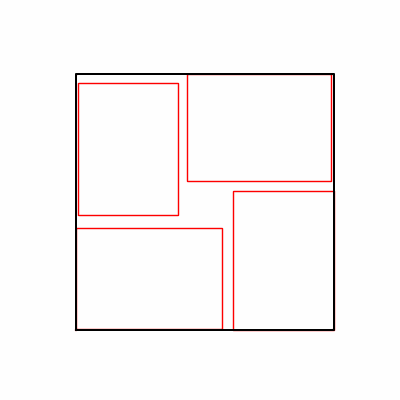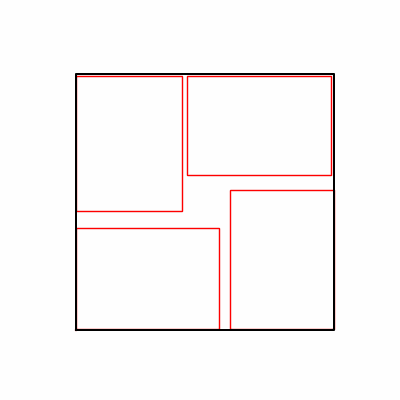
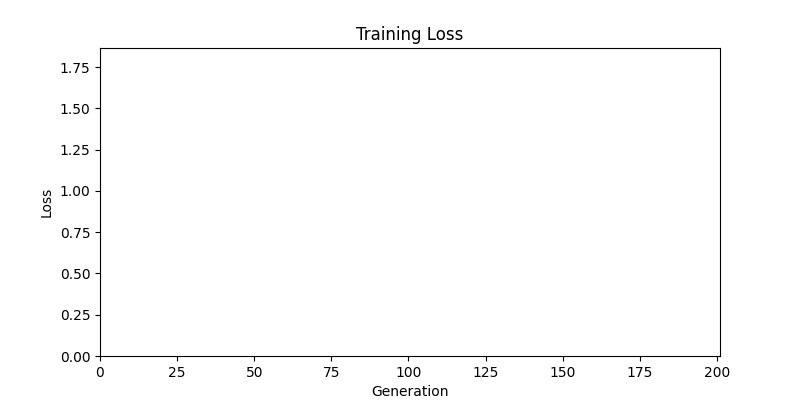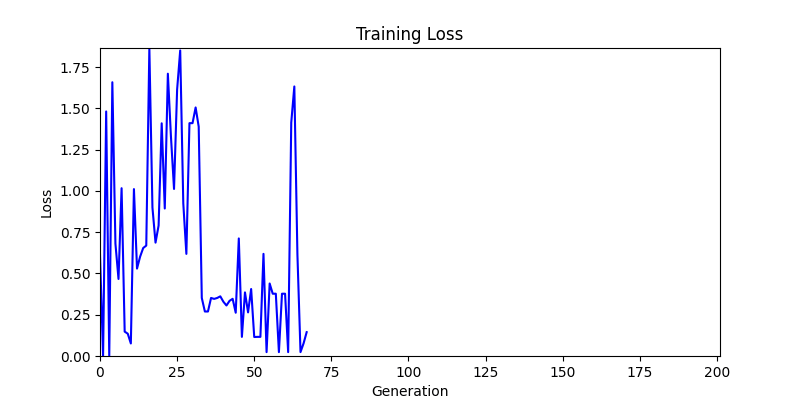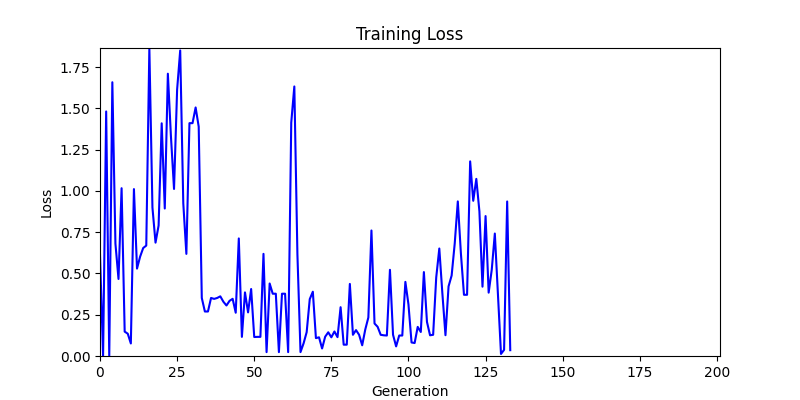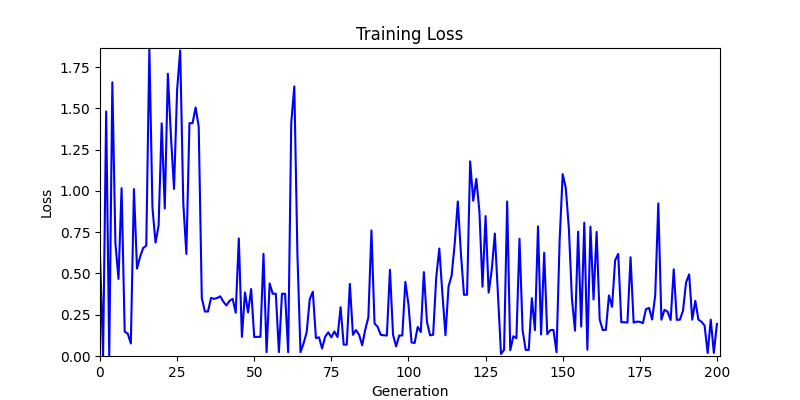
- 환경 2
Loss 1
Loss 2
Loss 3
Loss 4
Conclusion
- 미분 가능한 환경, 즉 파라미터의 변화에 따른 환경이나 결과의 변화가 연속적일 수록 최적화 과정에서 더 좋은 결과를 얻을 수 있음을 확인할 수 있었습니다.
- 이는 단순한 경사하강이나 AdamW 뿐만 아니라, 심지어 ga 와 같은 최적화 알고리즘에서도 같은 경향을 보였습니다.
- 모든 파라미터에 적용하는 것이 불가능할 때도 있지만, 이를 의식해 개발할 때 추가하고자 하는 파라미터에 가능하다면 최대한 환경이 미분 가능한 형태로 추가하는 것이 의미가 있음을 재확인할 수 있었습니다.
-
- 비슷한 점수를 얻기 위해 ga 에서는 훨씬 많은 수의 실행 횟수가 필요했습니다. ga 보다 효율적인 방법이 더 많을 수 있다는 것을 시사합니다. 미분 가능한 환경과 방법 혹은 또 다른 방법으로 전체 연산 횟수 또한 줄일 수 있을 것으로 기대합니다.
- 비슷한 점수를 얻기 위해 ga 에서는 훨씬 많은 수의 실행 횟수가 필요했습니다. ga 보다 효율적인 방법이 더 많을 수 있다는 것을 시사합니다. 미분 가능한 환경과 방법 혹은 또 다른 방법으로 전체 연산 횟수 또한 줄일 수 있을 것으로 기대합니다.
- Let’s Use Differentiable Environment!