Understanding Form Through Algorithms
Introduction
Contemporary science often reveals that the complex patterns we observe in nature actually arise from simple rules repeating and interacting. This phenomenon is called emergence, where each individual element behaves in a seemingly straightforward way, but together they form unpredictable and elaborate patterns or structures. Computer algorithms are exceptionally useful for exploring this phenomenon. By coding and simulating these rules, we can observe—step by step—how forms emerge, rather than just imitating nature or producing results. In other words, algorithms have evolved into a powerful methodology for analyzing the logic behind form generation.
Complexity Science and Algorithmic Models
Computational Models vs. Observed Forms
In complexity science, researchers build simplified computational models of natural phenomena based on rules, then run computer simulations and compare the simulated outputs to real-world observations. The goal isn’t to replicate the physical or chemical processes of nature exactly. Rather, it’s to capture the procedure by which forms emerge, and then progressively refine and re-run the experiments. By adjusting parameters and comparing each result to actual data, we gradually uncover how complicated forms arise. Hence, algorithms aren’t merely used to imitate nature but also serve as a key tool for understanding and analyzing shape formation.

D’Arcy Thompson and Alan Turing
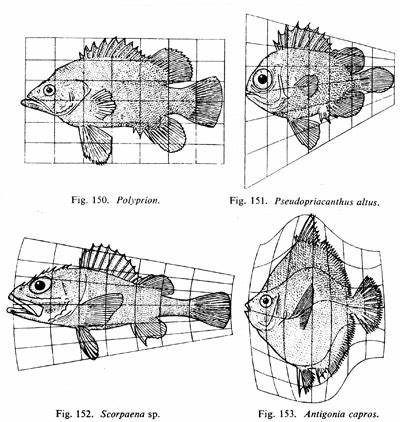
The view that shape generation can be understood through rule-based systems was systematically introduced in D’Arcy Wentworth Thompson’s On Growth and Form (1917). While Darwinian evolution dominated thinking at the time, Thompson emphasized the impact of physical forces on biological forms. He illustrated that structures like jellyfish bells or avian bone shapes could be explained using geometric and physical principles, and that fish body shapes, for instance, could be continuously transformed via grid transformations.
In 1952, mathematician Alan Turing proposed the reaction–diffusion model, showing that even extremely simple chemical reactions and diffusion processes could give rise to complex patterns like animal stripes or spots. This research was groundbreaking, demonstrating that genes don’t directly “paint” colors, but rather that local reaction rules spontaneously organize the pattern. This confirmed that emergence could derive from local rule interactions.
Major Algorithms for Explaining Natural Patterns
Scientists have harnessed these concepts to devise numerous algorithmic models that simulate and study form generation in nature.
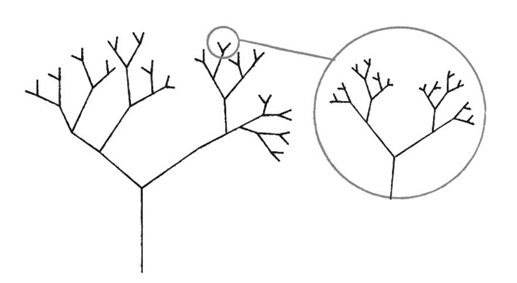
- Fractal Geometry and Self-similarity: Many structures in nature—such as tree branches, lightning, and Romanesco broccoli—exhibit fractal properties. When you zoom into a part of these forms, the smaller portion resembles the shape of the whole, a concept known as self-similarity. Benoît Mandelbrot’s fractal geometry shows that applying recursive rules can re-create even the seemingly boundless complexity of coastlines and mountain outlines.


- Cellular Automata: Conway’s Game of Life is a classic example. Each cell in a grid follows a simple local rule—living or dying based on the state of neighboring cells—yet over time, the overall system produces unexpectedly complex patterns. This hints that it’s possible to mimic phenomena like animal coat markings or city growth using only simple rules. Cellular automata illustrate how individual rules can lead to global complexity.


- Reaction-Diffusion Systems: Alan Turing’s theory proposed that patterns like spots or stripes emerge when two or more chemical substances react and diffuse at different rates, naturally creating stripes or spots. One chemical acts as an activator, while another acts as an inhibitor, and differences in their diffusion speeds lead to a pattern spontaneously dividing what was initially a uniform space. This type of model is widely used in biology, chemistry, and art to explain how intricate patterns form.

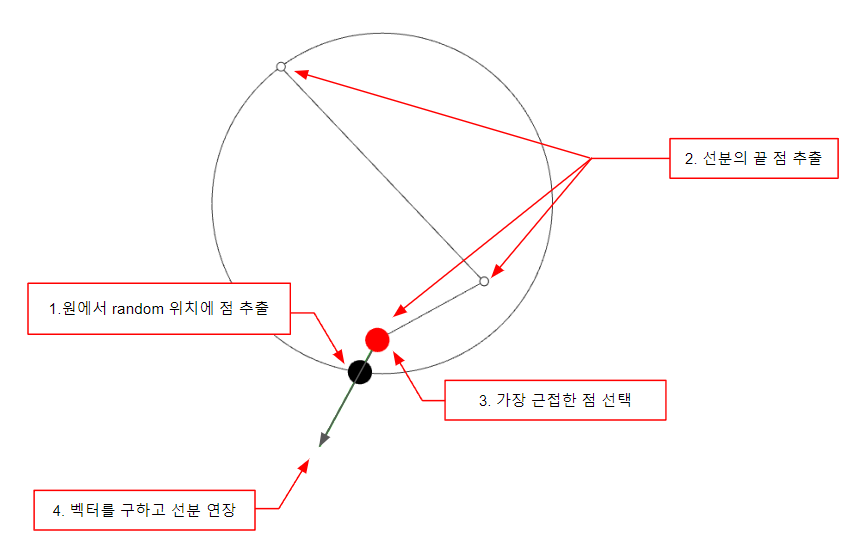
- Diffusion-Limited Aggregation (DLA): In this model, particles moving randomly will stick to a growing cluster, forming intricate branching or fractal-like crystal structures—similar to how lightning, frost, or mineral deposits form. Although each particle’s motion is random, the collective behavior results in branching growth.


These algorithmic approaches not only replicate the outward appearance of nature, but also serve as a tool for investigating the step-by-step logic by which forms develop.
Algorithmic Explanations of Design Forms
Applications in Design
Algorithms originally used to describe forms in nature also have significant relevance for design. In the past, algorithms might have been viewed mainly as tools for generating “complex and novel shapes,” but nowadays they’re also employed to analyze and explain why certain forms appear as they do:
- Making generative rules for shape creation explicit gives designs transparency and logical clarity.
- Iterative experimentation shows immediately how altering parameters changes the resulting form.
Richard Serra and Verb Lists
During the late 1960s, sculptor Richard Serra compiled a list of action verbs such as “to roll, to crease, to fold, to cut…” and applied them sequentially in his work. Each action (fold, cut, bend) might seem simple, but cumulatively, they produce intricate sculptural results. In algorithmic terms, each verb is a rule that transforms a shape in a specific way. If a computer were to simulate these steps, we could explicitly see: “Step 1 did X, Step 2 did Y, which led to this final shape.”

Hence, Serra’s sculptures are not just the product of artistic intuition—they can also be seen as the product of “a series of transformation rules.” An algorithmic model clarifies the logical mechanism behind the art-making process.
Parametric and Procedural Design
In parametric design, you don’t fix the final shape. Instead, you define parameters and rules (procedures). Suppose you specify column spacing, curvature, or height as inputs: the algorithm calculates the geometry in real time. Rather than controlling the shape directly, you focus on the rules that generate the shape.
- If you widen columns by 20%, you can quickly see how it alters the roof curve.
- Even in complex structures, as long as you know the rules and parameters, repeated testing and optimization become straightforward.
Thus, parametric design clarifies the intent behind the form and explains “why this shape resulted,” offering a transparent logical structure.
Examples of Action Verbs

Combining Creativity with Logic
Using algorithms to explain design doesn’t mean discarding artistic intuition. On the contrary, transforming a conceptual idea into explicit rules allows for rapid testing of “What if I tweak this parameter?”—leading to new possibilities. Design knowledge isn’t confined to a designer’s mind alone; it can become a transparent system that facilitates collaboration and verification.
Conclusion
Algorithmic approaches aren’t limited to researching natural phenomena; they’re equally powerful in creative fields, such as design, for clarifying how forms emerge and why they appear as they do.
- In nature, simple local rules can combine to produce emergent complexity.
- In design, focusing on parameters and rules makes generation processes more transparent and analyzable.
Through algorithms, we don’t just examine the final shape—we delve into how it was formed. By integrating artistic intuition with computational logic, we unlock both creative expansion and verifiable structures. Designers can conduct repeated experiments in much the same way that scientists explore optimal solutions. This algorithmic mindset bridges art and science, fostering broader collaboration and discourse, while shedding light on the underlying logic of form.