Infinite synthesis
Introduction
Deep Generative AI는 훈련 데이터와 유사한 새로운 데이터를 생성하는 인공지능 분야로, 텍스트 생성 및 이미지 생성뿐만 아니라 디자인 산업의 3D 모델 생성에도 영향을 미치고 있습니다. 건축 디자인 분야에서, 특히 초기 디자인 단계에서 Generative AI는 다양한 디자인 옵션을 검토하는 데 유용한 도구로 활용될 수 있습니다. 
Shou Sugi Ban / BYTR Architects
이 프로젝트는 잠재 벡터와 함께 딥 서명 거리 함수 모델(DeepSDF)을 활용하여, 훈련된 데이터와 유사한 무한한 수의 skyscrapers를 합성할 수 있는 알고리즘을 구축하는 것을 목표로 합니다. 이러한 벡터는 고차원 잠재 공간 내에 매핑되어 잠재적 skyscrapers를 합성하는 DNA 역할을 합니다. 건물의 형태를 표현할 수 있는 잠재 벡터를 조작하는 시스템을 통해 건축 디자이너는 다양한 디자인 옵션을 신속하게 생성하고 검토할 수 있습니다.
두 개 이상의 잠재 벡터 간의 조작(interpolation, and arithmetic operations)을 통해 모델은 가상으로 무한한 디자인 옵션을 제공합니다. 이 방법은 새로운 디자인 프로세스를 제공할 뿐만 아니라 기존의 디자인 방법론으로는 도달할 수 없었던 새로운 건축 형태를 탐구할 수 있게 해줍니다.
Understanding Signed Distance Functions
Wikipedia에서 Signed Distance Functions (SDFs)는 다음과 같이 정의됩니다:
수학과 그 응용분야에서 signed distance function(또는 oriented distance function)은 메트릭 공간에서 집합 \(\Omega\)의 경계까지의 한 점 \(x\)로부터의 수직 거리를 나타내며, 부호는 \(x\)가 \(\Omega\)의 내부에 있는지 여부에 따라 결정됩니다. 이 함수는 \(\Omega\) 내부의 점 \(x\)에서 양수 값을 가지며, signed distance function이 0이 되는 \(\Omega\)의 경계에 가까워질수록 값이 감소하고, \(\Omega\) 외부에서는 음수 값을 가집니다. 하지만 때로는 반대의 규칙(즉, \(\Omega\) 내부에서 음수, 외부에서 양수)이 적용되기도 합니다.
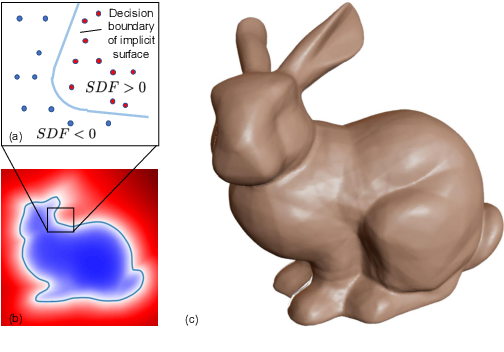
SDF representation applied to the Stanford Bunny
(a) 부호 결정 방법: 점이 표면에 있을 경우 SDF = 0
(b) signed distance field의 2D 단면
(c) SDF = 0에서 복원된 3D 표면
SDFs의 핵심은 복잡한 기하학적 형태를 표현하는 단순함과 강력함에 있습니다. 꼭지점, 모서리, 면을 사용하여 형태를 정의하는 전통적인 mesh 표현과 달리, SDFs를 사용하면 연속적인 표면을 가진 3D mesh 모델을 구축할 수 있으며, 이는 단지 3D 격자 형태의 XYZ와 해당하는 SDF 값만을 필요로 합니다.
SDF = 0에서 복원된 OMA의 CCTV 본사 건물의 다음 예시를 살펴보겠습니다. 초기에 SDF 값을 얻기 위해, CCTV 본사 모델 주변의 전체 공간이
아래 그림에서 볼 수 있듯이, 더 많은 격자점은 더 상세하고 정확한 3D 모델을 만들어냅니다. 예시에서 사용된 격자점의 수는 각각

Recovered CCTV headquarters from the SDFs
상단 3개, 원본 3D 모델 · resolution 8 · resolution 16
하단 3개, resolution 32 · resolution 64 · resolution 128
점이 모델의 내부인지 외부인지를 결정하는 각
수학과 그 응용분야에서 signed distance function(또는 oriented distance function)은 메트릭 공간에서 집합 \(\Omega\)의 경계까지의 한 점 \(x\)로부터의 수직 거리를 나타내며, 부호는 \(x\)가 \(\Omega\)의 내부에 있는지 여부에 따라 결정됩니다. 이 함수는 \(\Omega\) 내부의 점 \(x\)에서 양수 값을 가지며, signed distance function이 0이 되는 \(\Omega\)의 경계에 가까워질수록 값이 감소하고, \(\Omega\) 외부에서는 음수 값을 가집니다. 하지만 때로는 반대의 규칙(즉, \(\Omega\) 내부에서 음수, 외부에서 양수)이 적용되기도 합니다.

(a) 부호 결정 방법: 점이 표면에 있을 경우 SDF = 0
(b) signed distance field의 2D 단면
(c) SDF = 0에서 복원된 3D 표면
SDFs의 핵심은 복잡한 기하학적 형태를 표현하는 단순함과 강력함에 있습니다. 꼭지점, 모서리, 면을 사용하여 형태를 정의하는 전통적인 mesh 표현과 달리, SDFs를 사용하면 연속적인 표면을 가진 3D mesh 모델을 구축할 수 있으며, 이는 단지 3D 격자 형태의 XYZ와 해당하는 SDF 값만을 필요로 합니다.
SDF = 0에서 복원된 OMA의 CCTV 본사 건물의 다음 예시를 살펴보겠습니다. 초기에 SDF 값을 얻기 위해, CCTV 본사 모델 주변의 전체 공간이
regular grid에서 샘플링됩니다 (이 예시에서 resolution은 격자점의 수를 나타냅니다. 즉, resolution 8은 8x8x8 격자를 의미합니다). 각 격자점에서 SDF는 모델의 가장 가까운 표면으로부터의 점의 거리를 나타내는 값을 제공합니다. 모델 내부에서 이 값들은 음수(또는 규칙에 따라 양수)이며, 외부에서는 양수(또는 음수)입니다. 아래 그림에서 볼 수 있듯이, 더 많은 격자점은 더 상세하고 정확한 3D 모델을 만들어냅니다. 예시에서 사용된 격자점의 수는 각각
8x8x8(=512), 16x16x16(=4096), 32x32x32(=32768), 64x64x64(=262144), 128x128x128(=2097152)입니다. 격자점과 SDF 값을 사용하여 mesh를 복원하기 위해서는 Marching Cubes 알고리즘을 사용해야 합니다. 
상단 3개, 원본 3D 모델 · resolution 8 · resolution 16
하단 3개, resolution 32 · resolution 64 · resolution 128
점이 모델의 내부인지 외부인지를 결정하는 각
sign이 필요하기 때문에, SDF 값에서 복원하는 mesh는 완전히 닫힌 watertight mesh여야 합니다. 아래 코드를 사용하여 SDF 값과 각 격자 resolution에서 복원된 mesh를 검사했습니다. check_watertight 매개변수가 True로 설정되어 있어, 코드는 mesh가 watertight인지 확인하고, 완전히 닫혀있지 않은 경우 pcu를 사용하여 watertight mesh로 변환합니다.
mesh = DataCreatorHelper.load_mesh(
path=r"deepSDF\data\raw-skyscrapers\cctv_headquarter.obj",
normalize=True,
map_z_to_y=True,
check_watertight=True,
translate_mode=DataCreatorHelper.CENTER_WITHOUT_Z
)
for resolution in [8, 16, 32, 64, 128]:
coords, grid_size_axis = ReconstructorHelper.get_volume_coords(resolution=resolution)
sdf, *_ = pcu.signed_distance_to_mesh(
np.array(coords.cpu(), dtype=np.float32),
mesh.vertices.astype(np.float32, order='F'),
mesh.faces.astype(np.int32)
)
recovered_mesh = ReconstructorHelper.extract_mesh(
grid_size_axis,
torch.tensor(sdf),
)
Data preparation and processing
DeepSDF 모델을 훈련시키기 위한 데이터 준비의 첫 번째 단계는 skyscrapers의 3D 모델을 수집하는 것입니다. 저는 무료 3D 모델을 다운로드하기 위해 3dwarehouse를 사용했습니다. 3dwarehouse로부터 그림에 있는 모델들을 다운로드했습니다. 왼쪽부터, CCTV 본사 · 마하나콘 · 허스트 타워 · 중국은행 · 엠파이어 스테이트 빌딩 · 트랜스아메리카 피라미드 · 더 샤드 · 거킨 런던 · 타이페이 101 · 상하이 월드 파이낸셜 센터 · 원 월드 트레이드 센터 · 롯데 타워 · 킹덤 센터 · 차이나 준 · 버즈 알 아랍입니다. 제가 수집한 15개의 원본 데이터는 이 링크에 있습니다.

Skyscrapers
다음 단계는
(1) 정규화: 일반적으로 기하학적 데이터를 학습에 사용할 때는 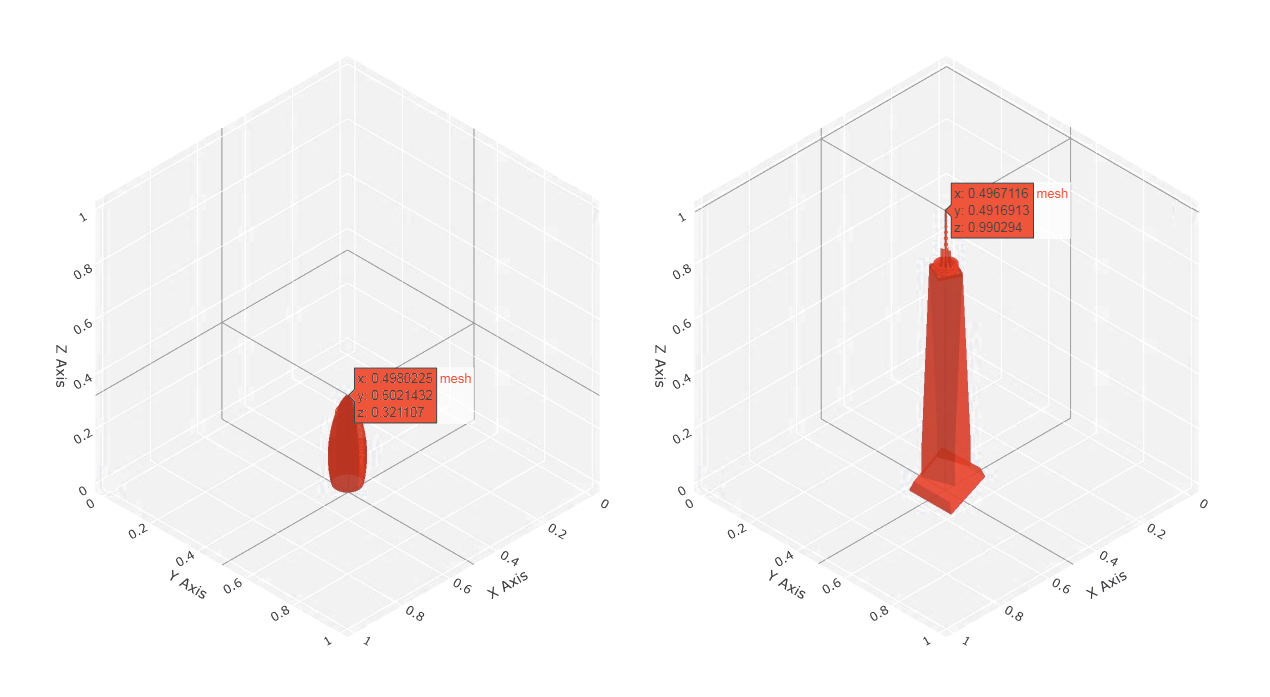
정규화된 skyscrapers들
왼쪽부터, 가장 낮은 건물(거킨 런던) · 가장 높은 건물(원 월드 트레이드 센터)
(2) 변환: DeepSDF 모델의 feed-forward network는 다음과 같은 구조를 가집니다. 다이어그램에서 "FC"로 표시된 8개의 fully connected layer로 구성되어 있습니다. 아래 그림에서 볼 수 있듯이, latent vector를 제외한 입력 X의 차원은 (x, y, z) 3으로 구성됩니다.
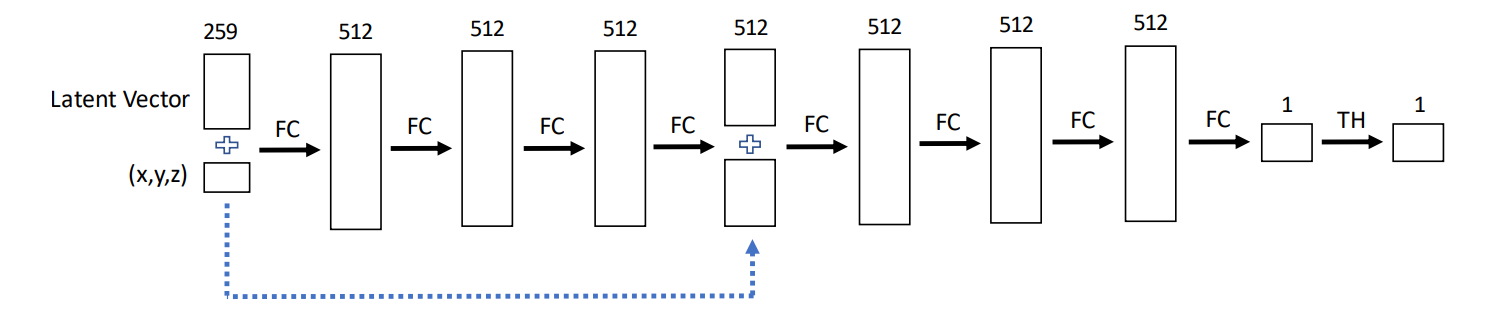
DeepSDF 모델을 위한 feed-forward network
데이터 샘플 \( X \)는 \( (x, y, z) \)와 해당하는 레이블 \( s \)로 다음과 같이 구성됩니다: \( X := \{(x, s) : SDF(x) = s\} \) 추가적으로, 각 샘플에 latent vector를 할당하기 위한 클래스 번호가 필요합니다. 서론 부분에서 언급했듯이, latent vector는 건물의 형태를 표현하는 DNA 역할을 합니다.

다음 단계는
(1) 정규화하여 모든 데이터를 regular grid 볼륨 내에 맞추고, (2) 변환하여 일관된 형식으로 만드는 것을 포함합니다. (1) 정규화: 일반적으로 기하학적 데이터를 학습에 사용할 때는
각각의 개별 객체에 대해 0과 1 사이의 값으로 정규화하고, 모델의 중심점을 원점(0, 0)으로 이동하여 정규화합니다. 즉, 모델의 가장 먼 점을 1로 설정합니다. 이러한 일반적인 정규화 방법을 사용하면 skyscrapers들의 상대적인 높이가 반영되지 않습니다. 따라서 이 프로젝트에서는 모든 skyscrapers 데이터 중 가장 높은 모델의 높이를 1로 설정하여 정규화했습니다. 
왼쪽부터, 가장 낮은 건물(거킨 런던) · 가장 높은 건물(원 월드 트레이드 센터)
(2) 변환: DeepSDF 모델의 feed-forward network는 다음과 같은 구조를 가집니다. 다이어그램에서 "FC"로 표시된 8개의 fully connected layer로 구성되어 있습니다. 아래 그림에서 볼 수 있듯이, latent vector를 제외한 입력 X의 차원은 (x, y, z) 3으로 구성됩니다.

데이터 샘플 \( X \)는 \( (x, y, z) \)와 해당하는 레이블 \( s \)로 다음과 같이 구성됩니다: \( X := \{(x, s) : SDF(x) = s\} \) 추가적으로, 각 샘플에 latent vector를 할당하기 위한 클래스 번호가 필요합니다. 서론 부분에서 언급했듯이, latent vector는 건물의 형태를 표현하는 DNA 역할을 합니다.
class SDFdataset(Dataset, Configuration):
def __init__(self, data_path: str = Configuration.SAVE_DATA_PATH):
self.sdf_dataset, self.cls_nums, self.cls_dict = self._get_sdf_dataset(data_path=data_path)
def __len__(self) -> int:
return len(self.sdf_dataset)
def __getitem__(self, index: int) -> Tuple[torch.Tensor]:
xyz = self.sdf_dataset[index, :3]
sdf = self.sdf_dataset[index, 3]
cls = self.sdf_dataset[index, 4].long()
return xyz.to(self.DEVICE), sdf.to(self.DEVICE), cls.to(self.DEVICE)
Implementing and training of DeepSDF model
위의
이 프로젝트에서는
순전파에 사용된
이제 학습 과정을 살펴보겠습니다. 모델은 150 에폭 동안 훈련되었으며, 전체 데이터(점의 수)는 64x64x64x15(=3932160)입니다. 이는 8:2 비율로 나뉘어 학습과 평가 과정에 사용되었습니다. 에폭당 평균 1000초가 소요되었습니다. 각 에폭 루프의 끝에서, 모델을 
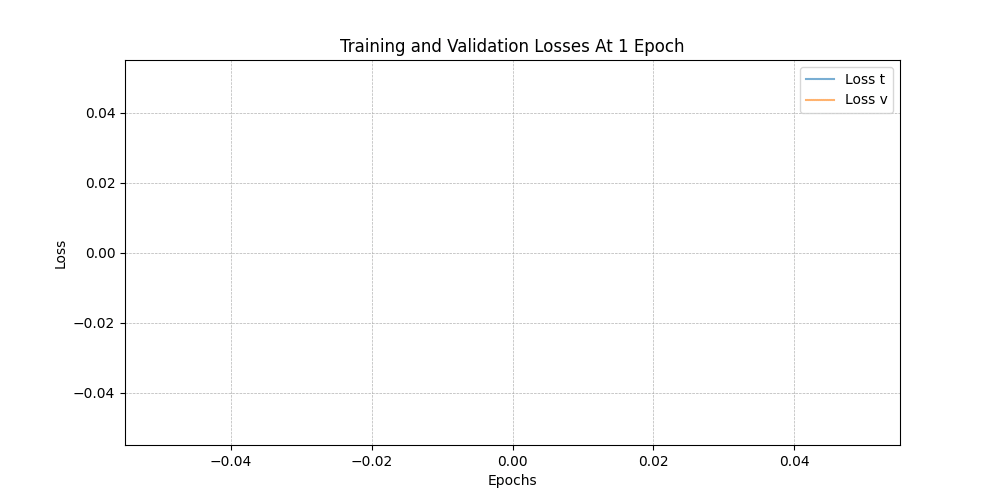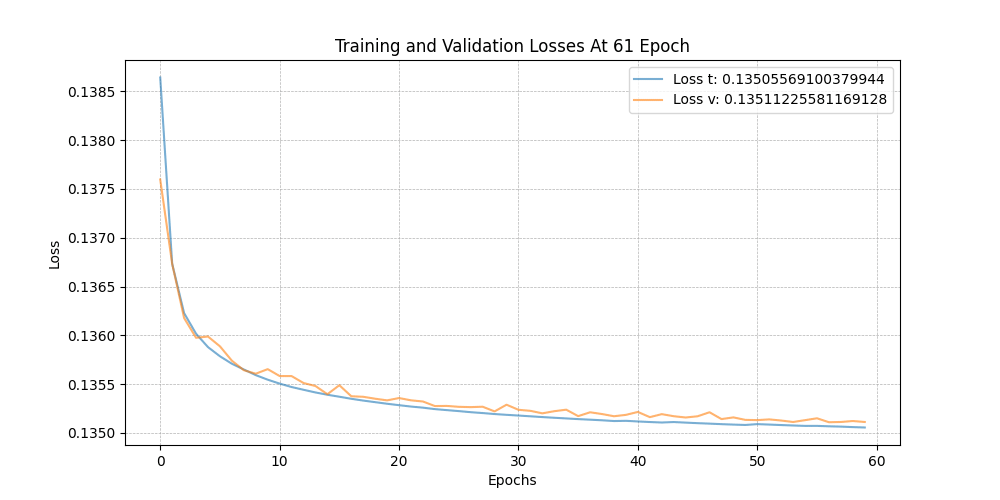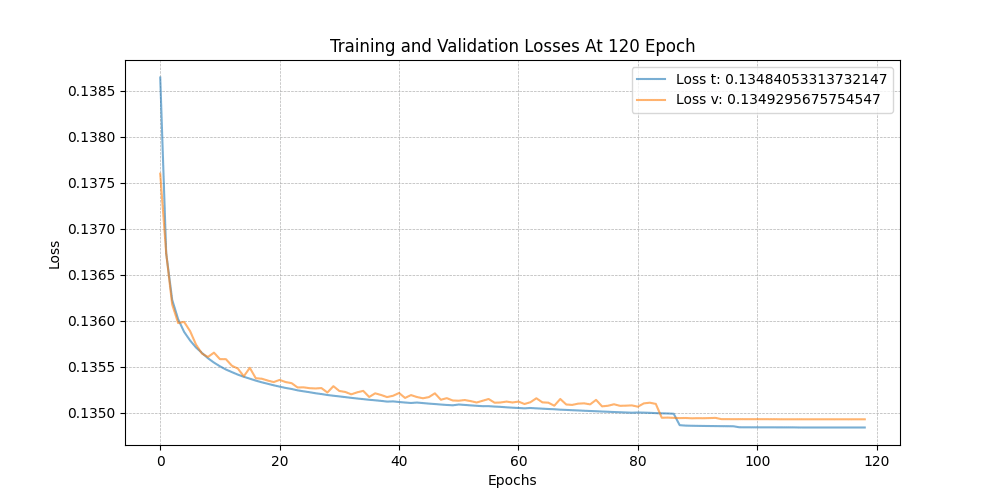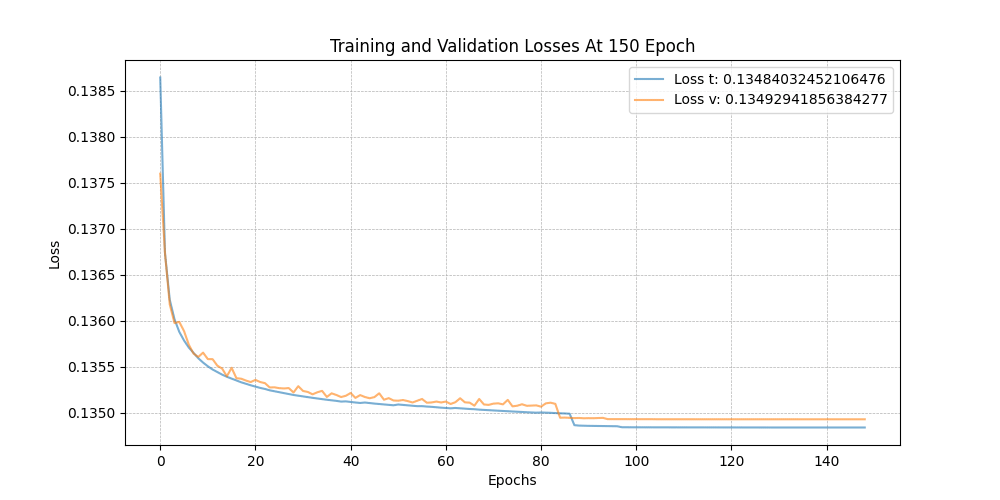
150 epochs 동안의 훈련 과정
위에서부터, 모델이 생성한 skyscrapers · 손실값
150 epochs 동안 모델을 훈련시킨 후, latent vector를 가진 15개의 skyscrapers에 대해 regular grid 점들의 각 점에서 SDF 값을 예측하여 3D 모델을 재구성했습니다. 아래 그림에서 왼쪽 열의 건물들은 모델에 의해 재구성된 것이고, 오른쪽 열의 건물들은 원본 3D 모델입니다.

모델이 생성한 skyscrapers와 원본 데이터 비교
모델이 정확한 디테일까지 재구성하지는 못하지만, 원본 skyscrapers과 유사한 건물을 적절하게 생성하는 것으로 보입니다. 이 모델 재구성 작업에서는 격자점 resolution으로 384x384x384(=56623104)를 사용했습니다.
(2) 변환 부분에서 볼 수 있듯이, DeepSDF 모델의 feed-forward network는 다음과 같습니다.
class SDFdecoder(nn.Module, Configuration):
def __init__(self, cls_nums: int, latent_size: int = Configuration.LATENT_SIZE):
super().__init__()
self.main_1 = nn.Sequential(
nn.Linear(latent_size + 3, 512),
nn.ReLU(True),
nn.Linear(512, 512),
nn.ReLU(True),
nn.Linear(512, 512),
nn.ReLU(True),
nn.Linear(512, 512),
nn.ReLU(True),
nn.Linear(512, 512),
)
self.main_2 = nn.Sequential(
nn.Linear(latent_size + 3 + 512, 512),
nn.ReLU(True),
nn.Linear(512, 512),
nn.ReLU(True),
nn.Linear(512, 512),
nn.ReLU(True),
nn.Linear(512, 1),
nn.Tanh(),
)
self.latent_codes = nn.Parameter(torch.FloatTensor(cls_nums, latent_size))
self.latent_codes.to(self.DEVICE)
self.to(self.DEVICE)
def forward(self, i, xyz, cxyz_1=None):
if cxyz_1 is None:
cxyz_1 = torch.cat((self.latent_codes[i], xyz), dim=1)
x1 = self.main_1(cxyz_1)
# skip connection
cxyz_2 = torch.cat((x1, cxyz_1), dim=1)
x2 = self.main_2(cxyz_2)
return x2
SDFdecoder 클래스는 다음과 같은 입력 인자를 가집니다: cls_nums는 skyscrapers의 수latent_size는 latent vector의 차원
이 프로젝트에서는
cls_nums와 latent_size를 각각 15와 128로 사용했습니다. 따라서 latent vector를 위해 초기화된 인스턴스 변수(self.latent_codes)의 크기는 torch.Size([15, 128])입니다. 순전파에 사용된
skip connection 기법은 네트워크가 학습한 고수준 특징과 저수준 정보(XYZ 좌표)를 결합하여 SDF를 표현하는 복잡한 함수를 학습할 수 있게 합니다. 이제 학습 과정을 살펴보겠습니다. 모델은 150 에폭 동안 훈련되었으며, 전체 데이터(점의 수)는 64x64x64x15(=3932160)입니다. 이는 8:2 비율로 나뉘어 학습과 평가 과정에 사용되었습니다. 에폭당 평균 1000초가 소요되었습니다. 각 에폭 루프의 끝에서, 모델을
정성적으로 평가하기 위해 skyscrapers을 재구성하는 코드를 추가했습니다. 

위에서부터, 모델이 생성한 skyscrapers · 손실값
150 epochs 동안 모델을 훈련시킨 후, latent vector를 가진 15개의 skyscrapers에 대해 regular grid 점들의 각 점에서 SDF 값을 예측하여 3D 모델을 재구성했습니다. 아래 그림에서 왼쪽 열의 건물들은 모델에 의해 재구성된 것이고, 오른쪽 열의 건물들은 원본 3D 모델입니다.

모델이 정확한 디테일까지 재구성하지는 못하지만, 원본 skyscrapers과 유사한 건물을 적절하게 생성하는 것으로 보입니다. 이 모델 재구성 작업에서는 격자점 resolution으로 384x384x384(=56623104)를 사용했습니다.
Synthesizing skyscrapers infinitely
마지막으로, skyscrapers들을 보간하거나 산술 연산을 사용하여 합성해보겠습니다. 다음 코드를 통해 초기 15개 건물의 latent vector를 합성하는 것으로 시작하여 다양한 형태의 무한한 데이터를 생성할 수 있습니다. 이번에는 이들을 합성하기 위해 128x128x128(=2097152) 격자점 resolution을 사용했습니다.
초기 15개의 skyscrapers를 사용해서 450개의 skyscrapers 합성
첫 번째 행의 사각형으로 표시된 것이 초기 15개의 skyscrapers
def infinite_synthesis(
sdf_decoder: SDFdecoder,
save_dir: str,
synthesis_count: int = np.inf,
resolution: int = 128,
map_z_to_y: bool = True,
check_watertight: bool = True,
):
synthesizer = Synthesizer()
synthesized_latent_codes_npz = "infinite_synthesized_latent_codes.npz"
synthesized_latent_codes_path = os.path.join(save_dir, synthesized_latent_codes_npz)
os.makedirs(save_dir, exist_ok=True)
synthesized_latent_codes = {
"data": [
{
"name": i,
"index": i,
"synthesis_type": "initial",
"latent_code": list(latent_code.detach().cpu().numpy()),
}
for i, latent_code in enumerate(sdf_decoder.latent_codes)
]
}
if os.path.exists(synthesized_latent_codes_path):
synthesized_latent_codes = {
"data": list(np.load(synthesized_latent_codes_path, allow_pickle=True)["synthesized_data"])
}
while len(synthesized_latent_codes["data"]) < synthesis_count:
print("synthesized data length:", len(synthesized_latent_codes["data"]))
if random.Random(time.time()).random() < 0.5:
selected_indices, synthesized_latent_code = synthesizer.random_arithmetic_operations_synthesis(
sdf_decoder=sdf_decoder, latent_codes_data=synthesized_latent_codes
)
synthesis_type = "arithmetic"
name = f"{selected_indices}.obj"
save_name = os.path.join(save_dir, name)
else:
(
selected_indices,
random_interpolation_factor,
synthesized_latent_code,
) = synthesizer.random_interpolation_synthesis(
sdf_decoder=sdf_decoder, latent_codes_data=synthesized_latent_codes
)
synthesis_type = "interpolation"
name = f"{selected_indices}__{str(random_interpolation_factor).replace('.', '-')}.obj"
save_name = os.path.join(save_dir, name)
if os.path.exists(save_name):
continue
_ = synthesizer.synthesize(
sdf_decoder=sdf_decoder,
latent_code=synthesized_latent_code,
resolution=resolution,
save_name=save_name,
map_z_to_y=map_z_to_y,
check_watertight=check_watertight,
)
synthesized_data = {
"name": name,
"index": len(synthesized_latent_codes["data"]),
"synthesis_type": synthesis_type,
"latent_code": list(synthesized_latent_code.detach().cpu().numpy()),
}
synthesized_latent_codes["data"].append(synthesized_data)
np.savez(
synthesized_latent_codes_path,
synthesized_data=np.array(synthesized_latent_codes["data"]),
)
clear_output(wait=False)

첫 번째 행의 사각형으로 표시된 것이 초기 15개의 skyscrapers
Tracking synthesized data
skyscrapers을 합성하는 데 사용된 위의 함수가 데이터를 기록하기 때문에, 우리는 이 데이터를 사용하여 합성된 skyscrapers들의 부모를 확인할 수 있습니다. 이 과정은 그래프 기반 분석을 사용하여 주어진 합성 디자인에서 그 기원까지 역추적하는 것을 포함합니다. 이를 통해 우리는
아래 그림들은 이러한 함수들의 적용을 보여주며, 초기 디자인에서 시작하여 다양한 합성 단계를 거쳐 복잡한 구조물로 완성되는 합성된 skyscrapers들의 추적과 시각화를 보여줍니다. 이는 합성된 skyscrapers들 내의 복잡한 관계와 의존성을 보여줍니다.
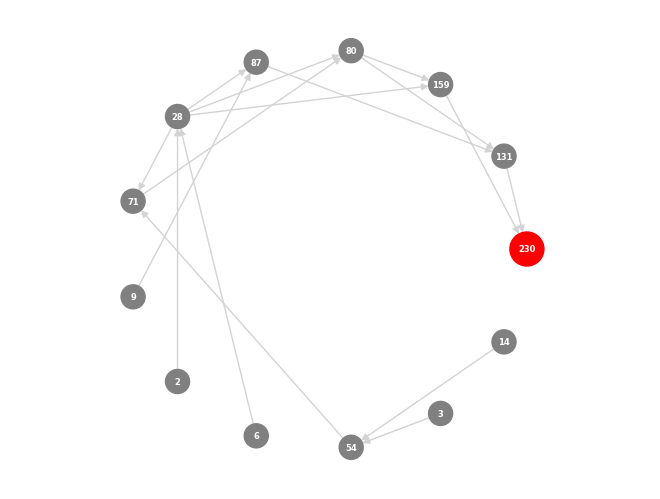
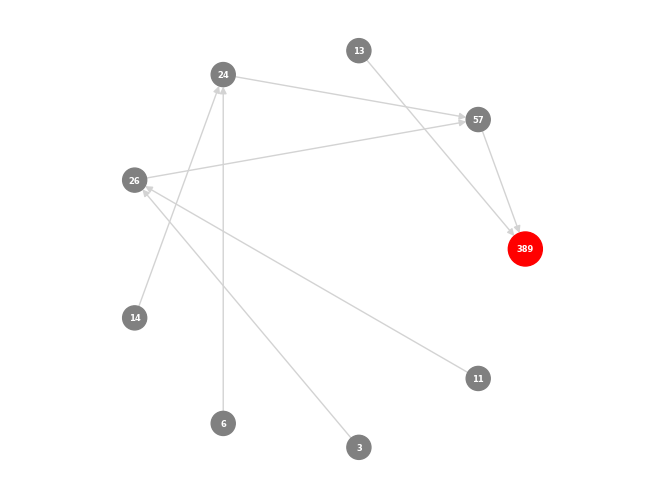
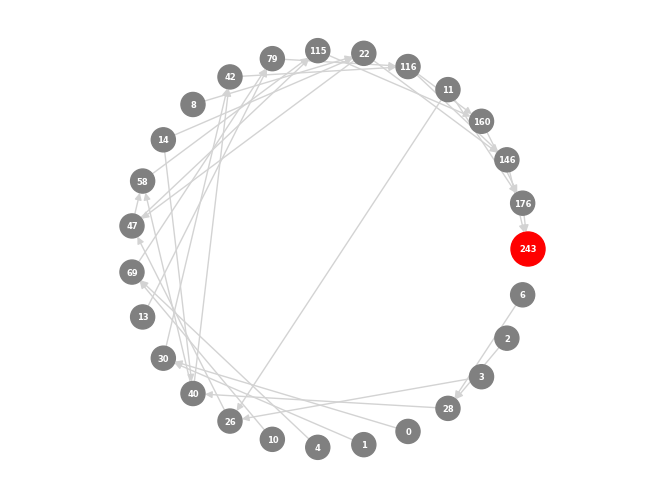
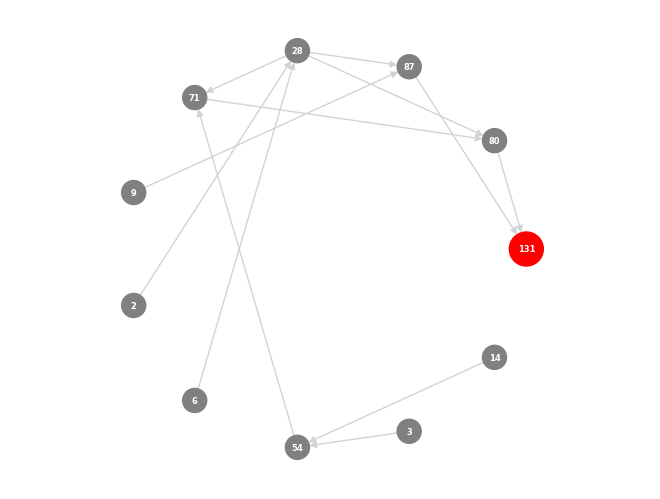
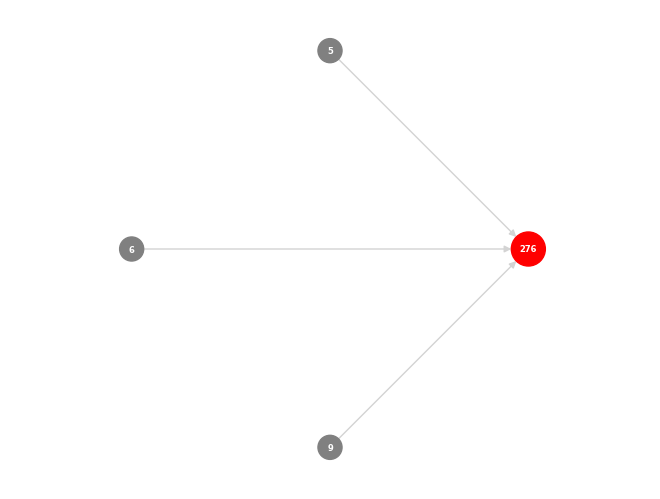
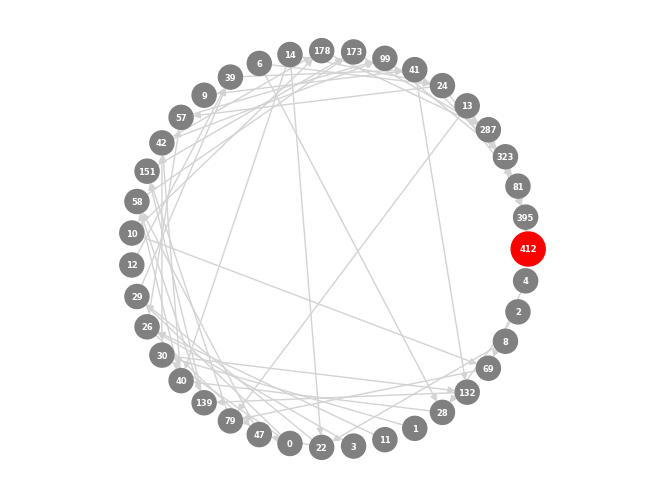
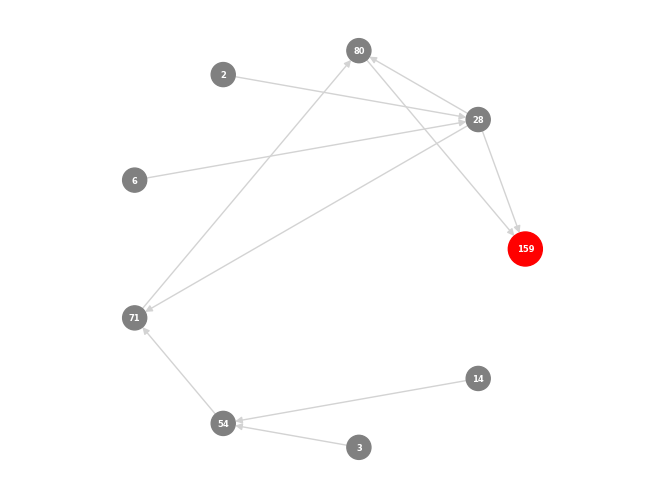
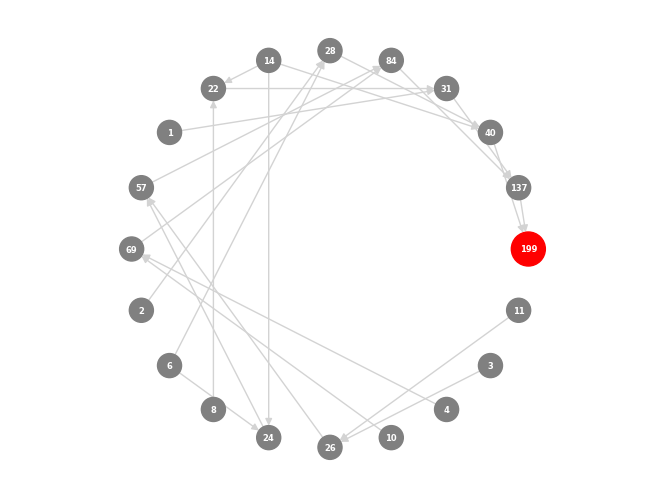
Tracking synthesized skyscrapers
특정 디자인이 어떻게 도출되었는지와 원본 모델이 합성 결과에 미치는 영향을 이해할 수 있습니다. 따라서 합성된 skyscrapers들을 추적하기 위해 BFS를 사용했습니다. 아래 그림들은 이러한 함수들의 적용을 보여주며, 초기 디자인에서 시작하여 다양한 합성 단계를 거쳐 복잡한 구조물로 완성되는 합성된 skyscrapers들의 추적과 시각화를 보여줍니다. 이는 합성된 skyscrapers들 내의 복잡한 관계와 의존성을 보여줍니다.








Limitations and future works
이 프로젝트는 skyscrapers 디자인을 합성하는 Deep Generative AI의 잠재력을 보여주지만, 한계점도 있습니다. 따라서 다음과 같은 점들이 개선되어야 합니다:
- 디자인 평가: 모델이 skyscrapers 디자인을 합성할 수 있지만, 현재는 이러한 디자인의 품질을 자동으로 평가하는 기능이 구현되어 있지 않습니다.
- 세부 표현: 현재 모델의 주요 한계점 중 하나는 skyscrapers 모델의 복잡한 세부 사항을 정확하게 포착하지 못한다는 것입니다.
- 컴퓨팅 자원: 모델 훈련 과정, 특히 상세한 합성을 위한 높은 해상도에서는 상당한 컴퓨팅 성능과 시간이 필요합니다.
- 대화형 디자인 도구: 건축가가 직접 latent vector를 조작하거나 제약 조건과 선호도를 지정할 수 있는 대화형 도구를 개발하면 실제 디자인 응용에서 이 기술을 더 실용적이고 매력적으로 만들 수 있습니다.
References
- https://en.wikipedia.org/wiki/Signed_distance_function
- https://github.com/fwilliams/point-cloud-utils
- https://scikit-image.org/docs/stable/auto_examples/edges/plot_marching_cubes.html
- https://xoft.tistory.com/47
- https://velog.io/@qtly_u/Skip-Connection
- https://arxiv.org/pdf/1901.05103.pdf
- https://github.com/facebookresearch/DeepSDF
- https://github.com/maurock/DeepSDF