Introduction

현대 과학에서는 자연의 복잡한 패턴이 사실은 단순한 규칙의 반복과 상호작용에서 발생한다는 사실이 자주 발견된다. 이를 창발성(emergence)이라고 부르는데, 개별 요소의 행동은 단순해 보여도 그 요소들이 모여 체계적으로 연결될 때 예측하기 어려운 복잡한 패턴이나 구조가 나타나는 현상을 의미한다. 컴퓨터 알고리즘은 이러한 과정을 살펴보기에 매우 적합하다. 왜냐하면 규칙을 프로그래밍해 시뮬레이션을 돌려 보면, 형태가 어떻게 만들어지는지 과정을 단계별로 추적할 수 있기 때문이다. 이는 자연을 단순히 흉내 내거나 결과물을 찍어내는 차원을 넘어, 형태가 생성되는 논리를 분석하는 강력한 방법론으로 발전한다.


Complexity Science and Algorithmic Models

Computational Models vs. Observed Forms

복잡계 과학(Complexity science)에서는 자연현상을 단순화한 계산 모델을 규칙 기반으로 구축하고, 이를 컴퓨터 시뮬레이션으로 돌려 나온 결과물을 실제 자연에서 관찰되는 형태와 비교함으로써 이론을 검증한다. 이때 알고리즘은 자연의 물리·화학적 과정을 똑같이 재현할 필요는 없다. 중요한 것은 형태가 생성되는 절차(procedure)를 포착하고, 그 과정을 조금씩 수정해가며 반복 실험하는 능력이다. 파라미터 값을 바꾸고, 얻어진 결과가 자연의 실측 데이터와 얼마나 유사한지 비교하는 식으로 진행하면, 복잡한 형태가 어떤 과정을 통해 발생하는지를 점진적으로 알아갈 수 있다. 따라서 알고리즘은 자연 모사가 아니라 형태를 이해하고 분석하기 위한 탐구 수단으로도 기능한다.

Flocking effect
Boid cohesion


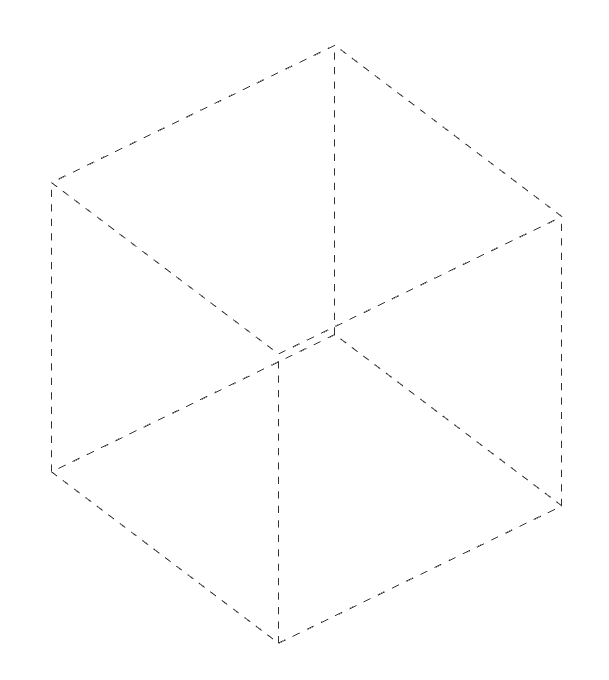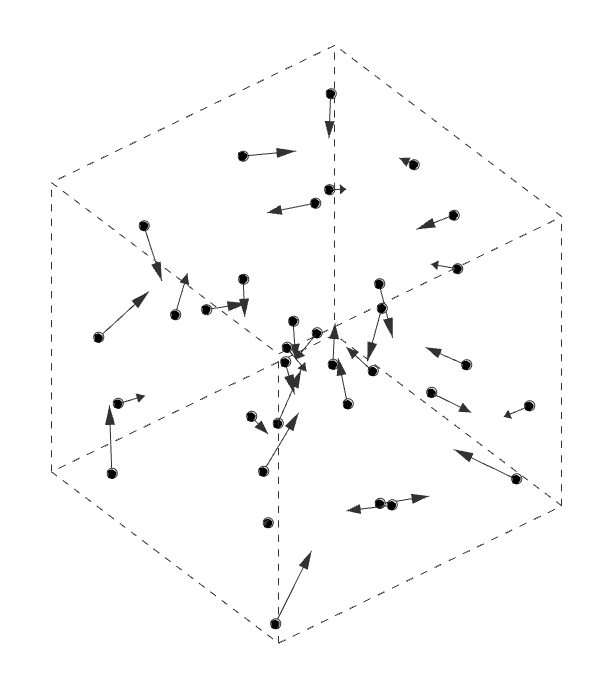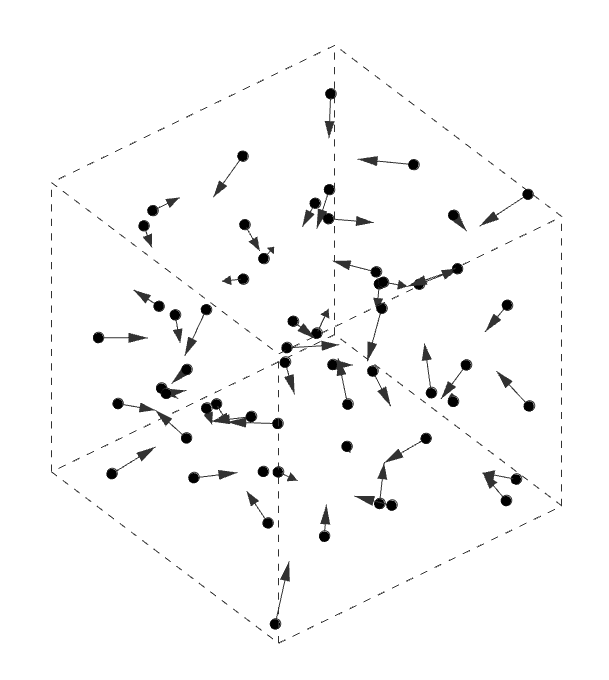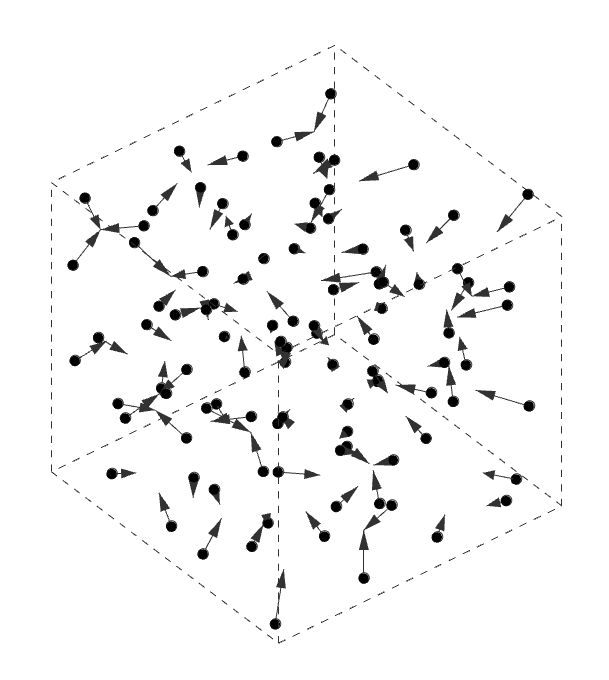
D’Arcy Thompson and Alan Turing

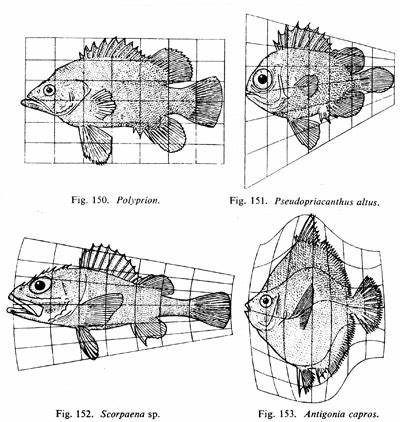
규칙 기반으로 형태생성을 이해하려는 관점은 다르시 톰슨(D’Arcy Wentworth Thompson)의 On Growth and Form(1917)에서 체계적으로 드러났다. 톰슨은 다윈적 진화가 강조되던 당시 분위기에서 더 나아가, 물리적 힘이 생물의 형태에 미치는 영향에 주목했다. 해파리 종 모양이나 새 뼈 구조가 기하학적·물리학적 원리로 설명될 수 있고, 어류의 체형은 격자변환(grid transformation)으로 서로 변형 가능한 사례가 될 수 있음을 제시했다.

이후 1952년 수학자 앨런 튜링(Alan Turing)은 반응-확산 모델을 제안해, 극도로 단순해 보이는 화학 반응과 확산만으로도 동물의 얼룩, 줄무늬 같은 복잡한 패턴이 형성될 수 있음을 수리적으로 증명했다. 이는 “유전자가 직접 색깔을 ‘그리는(paint)’ 것이 아니라, 국소적 반응 규칙이 패턴을 저절로 조직화한다”는 사실을 보여준 획기적인 연구로, 복잡한 형태 발생이 국소 규칙의 상호작용으로부터 창발할 수 있음을 확인시켰다.


Major Algorithms for Explaining Natural Patterns

과학자들은 이러한 원리를 바탕으로, 자연계에서 일어나는 형태 발생을 시뮬레이션하고 연구하기 위해 다양한 알고리즘적 모델을 고안했다.

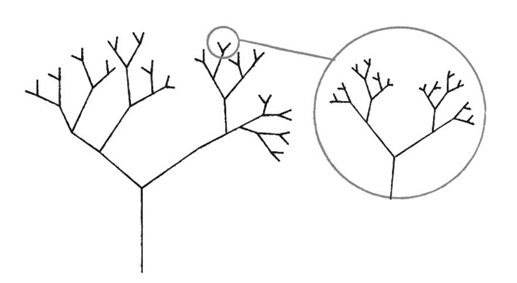
  • Fractal Geometry and Self-similarity: 자연에는 나뭇가지, 번개, 로마네스코 브로콜리처럼 프랙털 특성을 띠는 구조가 많다. 부분을 확대했을 때 전체와 유사한 형태가 반복되는 자기 유사성이다. 브누아 망델브로(Benoît Mandelbrot)의 프랙털 기하학은 단순한 재귀적 규칙을 반복 적용함으로써 해안선이나 산맥 윤곽 같은 ‘무한히 복잡해 보이는’ 패턴도 재현 가능함을 보여준다.
Fractal patterns


  • Cellular Automata: 콘웨이의 생명 게임(Game of Life) 등이 대표 예다. 격자 위 개별 셀이 국소적 규칙(이웃의 상태에 따라 생존·사멸 결정)만 지키며 진행되는데, 시간이 지날수록 복잡한 패턴이 출현한다. 이는 동물 무늬나 도시 성장 같은 자연·사회 현상을 단순 규칙으로 모사할 수 있음을 시사한다. 이때 알고리즘은 개별 규칙이 전체 복잡성을 어떻게 야기하는지 설명하는 핵심 도구가 된다.
Cellular Automata Zebra Patterns


  • Reaction-Diffusion Systems: 앨런 튜링이 제안한 이 모델은 두 가지 이상의 화학 물질이 상호 반응하고, 공간적으로 확산하는 과정에서 얼룩·줄무늬 같은 패턴이 만들어지는 원리를 설명한다. 한 물질이 활성, 다른 물질이 억제를 맡고, 이 둘의 확산 속도 차이가 균일했던 공간을 자연스레 분할한다. 실제 동물 피부의 얼룩무늬와 유사한 패턴도 충분히 재현할 수 있어, 생물학·화학·예술 전반에서 광범위하게 쓰인다.
Diffusion limited aggregation


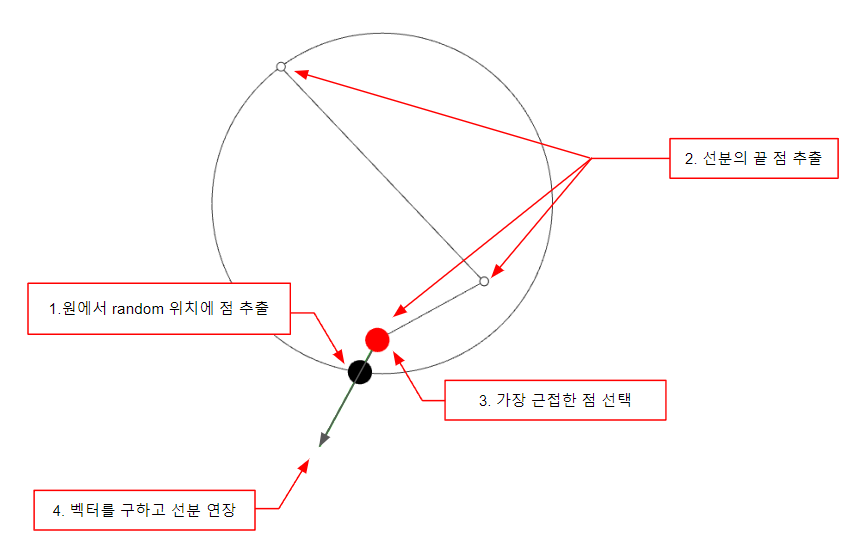
  • Diffusion-Limited Aggregation (DLA): 무작위 운동을 하는 입자들이 군집 중심에 달라붙으며 결정체를 성장시키는 방식이다. 번개나 서리, 광물 결정이 나뭇가지형·프랙털형 구조를 띠는 이유를 보여준다. 무작위 운동이라는 단순 규칙이 여러 입자에 걸쳐 적용될 때, 전체적으로는 나뭇가지 구조가 창발한다.


이러한 알고리즘들은 자연의 외형을 복제하는 데만 머물지 않고, 형태가 단계별로 생성되는 논리를 파악하고 분석하는 수단으로 활용된다..


Algorithmic Explanations of Design Forms

Applications in Design

자연의 형태를 설명하는 데 활용되던 알고리즘들은 디자인에서도 의의가 크다. 과거에는 “복잡하고 참신한 형태를 생성하는 도구” 정도로 주로 인식됐지만, 요즘에는 “왜 그 형태가 그렇게 생겼는가”를 분석하고 설명하는 방법으로도 쓰인다.

  • 형태 생성 규칙을 명시적으로 표현하면, 디자인 결과물의 논리가 투명해진다.
  • 반복 실험을 통해 “어떤 파라미터 변화가 어떤 형태 변화를 유발하는지” 즉각 확인할 수 있다.


Richard Serra and Verb Lists

조각가 리처드 세라는 1960년대 말, ‘to roll, to crease, to fold, to cut…’ 같은 행동 동사를 리스트로 만들어 작업 과정에 적용했다. 각 동사는 ‘자르고, 접고, 구부리는’ 식의 단순 조작이지만, 이들이 순차로 누적되면 복잡한 조형물이 탄생한다. 알고리즘으로 보면, 각 동사가 “형태를 특정 방식으로 변환하는 규칙”에 해당한다. 만약 이를 컴퓨터로 시뮬레이션한다면, “1단계에서 무엇을 하고, 2단계에서 어떤 변환을 적용했기에 최종 결과가 이 형태가 되었는가?”라는 과정을 명료하게 시각화·기록할 수 있다.


즉, 세라의 조각은 예술적 영감만이 아니라 “연속된 변환 규칙들이 만든 결과물”로도 볼 수 있다. 알고리즘은 이 변환 과정을 명시화하여, 작품의 생성 메커니즘을 논리적으로 설명하는 틀을 제공한다.


Parametric and Procedural Design

파라메트릭 디자인에서는 형상을 직접 고정하지 않고, 대신 파라미터와 규칙(프로시저)를 설정한다. 예컨대 기둥 간격, 곡률, 높이 등의 파라미터를 입력으로 주면, 알고리즘은 이 값들을 바탕으로 즉시 건축 형상을 재계산한다. 이는 형상 자체가 아니라 형상을 만드는 규칙을 중심에 두는 방식이다.

  • 설계자는 “기둥 간격을 20% 넓히면 지붕 곡률이 어떻게 변하는지”를 즉각 파악할 수 있다.
  • 복잡한 구조에서도 규칙과 파라미터만 알면 반복 실험과 최적화가 쉽다.결과적으로 이 방식은 설계 의도를 구조화하고, “왜 이런 형태가 나왔는지”를 설명할 수 있는 논리를 명확하게 제시한다.


Examples of Action Verbs


From the left, to split, to fill action verbs


Combining Creativity with Logic

알고리즘을 통해 디자인을 설명한다는 것은 직관이나 감각적 판단을 배제한다는 뜻이 아니다. 오히려 감각적 아이디어를 명시적 규칙으로 전환해, ‘만약 이 값을 이렇게 바꾼다면?’ 같은 가설을 빠르게 테스트함으로써 새로운 가능성을 열어준다. 이는 디자인 지식이 디자이너 개인의 머릿속에만 머무르지 않고, 협업과 검증이 쉬운 명시적 체계로 자리 잡는 효과를 낸다.


Conclusion

알고리즘적 접근은 자연 현상을 연구할 때만 유효한 것이 아니라, 디자인을 포함한 창작 영역 전반에서 “형태가 어떻게 만들어지고, 왜 그렇게 생겼는지”를 해명하는 데 큰 도움을 준다.

  • 자연에서는 간단한 국소 규칙이 서로 얽혀 창발성을 일으켜 복잡한 패턴을 만든다.
  • 디자인에서도 파라미터와 규칙에 주목해, 형태 생성 과정을 투명하게 기록하고 분석할 수 있다.

알고리즘을 통해 우리는 결과물만 보지 않고 과정 자체를 다룬다. 이는 직관적 감각과 계산적 논리를 융합해, 창의적 확장과 검증 가능한 구조를 동시에 확보하는 길을 열어준다. 디자이너가 실험을 거듭하며 최적 해법을 찾듯이, 형태 생성 알고리즘도 다양한 조건을 시험해볼 수 있다. 결국 이런 알고리즘적 사고는 예술과 과학을 연결하고, 협업과 토론의 장을 넓혀주며, 형태가 가진 내재적 논리를 더욱 명료하게 밝혀줄 것이다.